PROPOSITIO XXII
167 Sumpto spatio sub spira secundae revolutionis et sub recta, quae secunda est in revolutionis initio, potest figura circumscribi et inscribi, ita ut circumscripta et inscripta ex frustis similibus sint compositae, et id, quo haec ab illa exceditur, quocumque dato spatio minus sit.
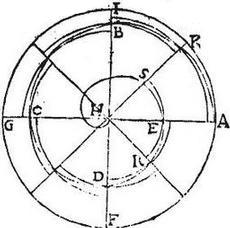
168 Sit spira secundae revolutionis ABCDE, eius initium H, initium revolutionis AH, linea secunda in revolutionis initio sit EA, circulus secundus AFG eius diametri AG, FI se invicem orthogonaliter secantes. 169 Oportet spatio contento sub spirali ABCDE rectaque AE, figuram circumscribere et inscribere, sicut proponitur. Secentur anguli recti diametrorum singuli per medium, iterum atque iterum, donec deveniatur ad frustum minus dato spatio. Sitque frustum tale sector circuli AHK et ducantur circulares peripheriae, sicut in praecedenti, per omnes sectiones diametrorum et spirae: quibus ordine peractis, ecce demonstrari potest, quod proponitur. 170 Siquidem figura circumscripta constat ex octo frustis similibus, (in apposito schemate V.G. ) sunt similes circuli sectores, figura vero inscripta constat ex totidem frustis similibus. 171 Nam frusta circumscriptae excedunt peripheriam spiralem, frusta vero inscriptae cadunt intra peripheriam spiralem. Cumque septem frusta inscriptae sint aequalia septem frustis circumscriptae (demptis scilicet maximo frusto circumscriptae et inscrip[S:216]tae) iam circumscripta excedet inscriptam eo excessu, quo maximum frustum circumscriptae AHK excedit minimum inscriptae RHE, quod est spatium SEAK minus scilicet dato spatio, cum et totum AHK minus sit dato spatio. Et hoc possibile factu conclusum est.
COROLLARIUM
172 Quare constat figuram talem circumscriptam addere posse super spiralem spatium, sive spiralem aream minus quocumque dato spatio, et ipsum spirale spatium addere posse super figuram inscriptam minus quocumque dato spatio. 173 Et eadem fieri posse in assumpto spatio sub spira tertiae, quartae, et quotaecumque revolutionis, et rectae a numero revolutionum dicta compraehenso.