PROPOSITIO XV

105 Lineae rectae, ab initio spiralis ad spiram secundae revolutionis eductae erunt ad invicem, sicut dictae peripheriae una cum tota peripheria circuli sumptae.

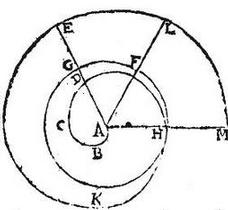
106 Sit, ut prius, spira primae revolutionis <ABCH, secundae autem¹²> HLM in quam incidant rectae AE, AL. 107 Dico quod linea AE ad lineam AL est sicut peripheria HKG una cum tota circuli peripheria, ad peripheriam HKF una cum tota cir[S:207]culi peripheria. Nam, quo tempore punctum H peregit totam circuli peripheriam, et insuper peripheriam HKG, eodem, et punctum A permeavit lineam AE. Item, quo tempore punctum H peragravit integram circuli peripheriam, et insuper ipsam peripheriam HKF, eodem, et punctum A percurrit lineam AL. Quare, per 2^<am> huius, erit sicut HKG peripheria cum tota peripheria, ad HKF peripheriam cum tota circuli peripheria, sicut linea AE ad lineam AL. Quod erat demonstrandum.

SCHOLIUM

108 Similiter, et lineae in spiram tertiae revolutionis cadentes, erunt ad invicem, sicut dictae peripheriae, cum tota [singulae¹³] circuli peripheria bis sumpta. 109 In spiram quartae revolutionis, cum circuli peripheria ter sumpta. 110 In spiram quintae revolutionis, cum circuli peripheria quater sumpta, et eodem deinde ordine, secundum numerum, unitate minorem numero revolutionum. Idem demonstrabitur, si altera eductarum linearum in terminum spirae inciderit.