PROPOSITIO XXXIII.

Pyramis, et conus sub aequis fastigiis sunt ad invicem sicut bases.

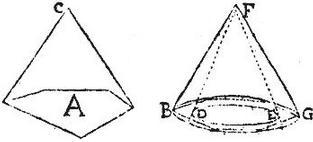
Sit pyramis AC super basim rectilineam A. Item conus BGF super circulum BG eiusdem altitudinis: aio quod sicut est rectilineum A ad circulum BG, sic est pyramis AC ad conum BGF: sit enim, si possibile est, pyramis AC ad conum BGF: sicut rectilineum A ad circulum maiorem, minoremve ipso circulo BG. Et primo minorem, qui sit DE concentricus ipsi BG, et ipsi BG inscribatur rectilineum polygonium per 13.12. laterum minime tangentium circulum DE, et super rectilineum BG intelligatur pyramis eiusdem altitudinis cum cono BGF eiusdem verticis: eritque per 7.12. sicut rectilineum A ad rectilineum BG, sic pyramis AC ad pyramidem BGF: sed per 8.5. maior est proportio rectilinei A ad circulum DE, quam rectilinei A ad rectilineum BG. Igitur maiorem rationem habet per 12.5. pyramis AC ad conum BGF, quam pyramis AC ad pyramidem BGF: ergo per 10.5. pyramis BGF maior est cono BGF, pars toto, quod est impossibile. Non est ergo pyramis AC ad conum BGF, sicut rectilineum A ad circulum aliquem minorem BG. Sed nec maiorem: sit enim, brevitatis causa, circulus, conusque propositus DEF eiusdem altitudinis cum pyramide AC. Aio quod pyramis AC ad conum DEF non erit sicut rectilineum A ad circulum quempiam maiorem ipso DE circulo, ut puta ad circulum BG. Ponatur enim BG circulus ipsi DE concentricus, et inscribatur, ut prius circulo BG rectilineum laterum minime tangentium circulum DE, et super rectilineum BG intelligatur pyramis eiusdem verticis cum cono DEF. Itaque quoniam sicut rectilineum A ad circulum BG, sic pyramis AC ad conum DEF: et per 7.12. sicut rectilineum A ad rectilineum BG, sic pyramis AC ad pyramidem BGF, atque maior est ratio rectilinei A ad rectilineum BG quam eiusdem rectilinei A ad circulum BG per octavam 5. propterea per 12.5. maiorem rationem habet pyramis AC ad pyramidem BGF, quam eadem pyramis AC ad conum DEF: ergo per 10.5. conus DEF maior est pyramide BGF, pars toto; quod est impossibile. Similiter non erit pyramis AC ad conum BGF sicut rectilineum A ad circulum quempiam maiorem ipso circulo BG: sec nec minorem, ut fuit ostensum: superest ergo ut pyramis AC ad conum BGF sit sicut rectilineum A ad circulum ipsum BG: quod est propositum. [S:81]

COROLLARIUM I.

Manifestum est quod prisma, et cylindrus sub aequalibus fastigiis sunt ad invicem sicut bases: namque tam prisma ad suam pyramidem per 8.12. quam cylindrus ad suum conum per 9. eiusdem triplus est.

COROLLARIUM II.

Itaque pyramis, et conus, quorum bases, et celsitudines sunt aequales, erunt ad invicem aequales. Hoc idem de prismate, et cylindro pronunciandum.