PROPOSITIO XXIII.
Solidum quod a triangulo circa unum laterum fixum, donec ad locum suum redeat, circumducto describitur, aequale est ei cono, cuius basis aequalis est conicae superficiei ab altero laterum trianguli circumductorum descriptae, altitudo autem aequalis perpendiculari ad idem latus cadenti ab angulo opposito: quin etiam si ab altero terminorum lateris fixi ad oppositum latus linea utcunque ducatur, solidum a triangulo abscisso descriptum aequale est ei cono, cuius basis aequalis est conicae superficiei descriptae a segmento lateris abscissi: altitudo autem aequalis est perpendiculari ad idem latus a dicto termino lateris fixi. Adhuc, si latus trianguli aequidistet axi, circa quem circumducitur triangulum, solusque trigoni angulus in axe terminetur: descriptum a triangulo solidum aequale erit ei cono, cuius basis aequalis est cylindricae superficiei descriptae a latere axi aequidistante; celsitudo autem aequalis perpendiculari ad idem latus ab axe ipso delapsae.

Brevissime hanc trifariam propositionem ostendam: sit namque trigonum ABG quod circa unum laterum, ut puta circa latus AB tanquam axem semel circumductum describat solidum AGB: ab angulo autem opposito AG, ut puta B ad latus oppositum AG, cadat perpendicularis BD. Sitque conus H, cuius basis sit aequalis conicae superficiei, quam describit latus AG; celsitudo vero aequalis perpendiculari BD. Aio quod conus H aequalis est solido AGB: ponatur enim primo trigonum ABG rectum angulum habens, qui apud B; et tunc per definitionem coni, solidum ABG a triangulo descriptum est conus, cuius axis AB, basisque semidiameter BG: quare per 3. huius. superficies conica, quam describit linea AG; et ideo basis coni H illi aequalis, ad basim coni ABG, sicut linea AG ad semidiametrum BG; et ideo propter triangulorum AGB, ABD similitudinem, sicut axis AB ad perpendicularem BD quae celsitudo est coni H. Itaque conorum AGB, et H bases sunt celsitudinibus mutuae; aequales ergo sunt per 12.12. coni AGB, et H: quod est propositum.
Ponatur nunc anguli trigoni ABG qui apud A, B acuti, et demittatur a puncto G perpendicularis ad AB axem linea GE; quae in revolutione trianguli ABG describet circulum, cuius semidiameter GE, eritque solidum AGB compositum ex duobus conis AGE, BGE communem basem habentes circulum, cuius semidiameter GE: sit itaque conus K basim dicto circulo aequalem habens, celsitudinem vero aequalem ipsi AB, eritque per praecedentem. aequalis conus K conis AGE, BGE simul sumptis, et proinde solido AGB. Itaque quoniam per 3. superficies conica, quam describit linea AG, et ideo basis coni H illi aequalis ad basim coni AGE, et ideo ad basim coni K illi aequalem, est sicut AG ad GE, et ideo propter triangulorum AGE, [S:67] ABD similitudinem, sicut AB celsitudo coni K ad BD celsitudinem coni H: ideo per 12.12. aequalis est conus H cono K, et ideo solido AGB: quod est propositum.
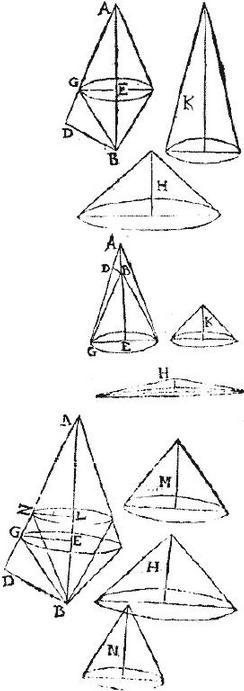
Demum in tertia descriptione ponatur ex angulis trianguli ABG, qui apud B obtusus, et tunc cadat a puncto G perpendicularis ad axem AB productum, qui sit GE ut in ambitu trianguli, linea GE circulum describat, qui basis erit tam coni AGE a triangulo AGE descripti, quam coni BGE a triangulo BGE descripti. Sit itaque conus K basim habens dicto circulo aequalem, et celsitudinem rectae AB: eruntque per praemissam. conus K, et conus BGE simul sumpti aequales cono AGE; communis utrinque auferatur conus BGE, et supererit conus K aequalis solido, quod in ambitu describitur per triangulum ABG. Itaque quoniam per 3. superficies conica, quam describit linea AG, et ideo basis coni H illi aequalis ad basim coni AGE, et ideo ad basim coni K illi aequalem est, sicut AG ad GE, et ideo propter triangulorum AGE, ABD similitudinem, sicut AB celsitudo coni K ad BD celsitudinem coni H. per 12.12. aequalis est conus H cono K, et ideo solido AGB: quod est propositum. Hactenus demonstratum est primum ex propositis.
Alterum sic se habet. In ipso triangulo ABG ab altero terminorum AB, qui sit B ducatur ad oppositum latus linea BZ; sitque conus N habens basim aequalem conicae superficiei, quam in circumductione describit linea GZ, et celsitudinem aequalem perpendiculari BD. Aio quod conus N aequalis est solido, quod in ambitu describitur a trigono BGZ. Sit enim conus H basim habens aequalem conicae superficiei, quam describit linea AG, et celsitudinem BD; item conus M basim habens aequalem conicae superficiei, quam describit linea AZ, et celsitudinem BD: eritque ut ostensum est, conus H aequalis solido descripto per trigonum ABG, conus autem M aequalis solido descripto per trigonum ABZ. Item quoniam conica superficies, quam describit linea AG aequalis est conicis superficiebus simul sumptis, quas describunt linea AZ, et linea ZG. Ideo basis coni H, [S:68] quae fuit aequalis illi conicae, aequalis erit basibus conorum, M, N simul sumptis, quorum scilicet bases his conicis fuerunt aequales, cumque conorum H, M, N, sit una celsitudo, erit per antepraemissam, conus H aequalis conis M, N, simul sumptis. Itaque de cono H, et solido AGB invicem aequalibus, auferatur conus M, et solidum AZB invicem aequalia: et supererunt conus N, et solidum descriptum a triangulo BGZ invicem aequalia, quod est propositum.

Superest tertia propositionis pars: circumducatur ut prius trigonum BGZ circum axem AB, sitque GZ latus ipsi AB parallelum, et conus H habeat basim aequalem cylindricae superficiei, quam describit linea GZ, celsitudinem vero aequalem perpendiculari BD ab angulo B ad latus GZ. Aio quod conus H aequalis est solido, quod describitur a triangulo BZG circumducto: compleatur enim rectangulum AZGX, quod in revolutione describet cylindrum, cuius axis AX, et basium semidiametri AZ, GX. Unde et BD circulum describet, qui terminus erit cylindrorum AD, DX; quin etiam triangula ABZ, BGX describent conos, quorum bases, quae et cylindri, et quorum vertex B. Sit itaque conus K basim quidem habens aequalem basi cylindri AG, celsitudinem vero duplam ipsius AX; eritque per 11.12. conus K, duplus coni habentis basim eandem, et axem AX: sed hic conus per praemissam, aequalis est conis AZB, BGX simul sumptis: ergo conus K duplus est ad conos AZB, BGX simul sumptos; sed eorumdem conorum AZB, BGX simul sumptorum duplum est solidum a triangulo BGZ descriptum: quando per 9.12. totus cylindrus AG triplus est eorundem conorum. Itaque aequalis est conus K solido per triangulum BGZ descripto.
At cum cylindrica superficies, quam describit linea GZ, et ideo basis coni H ei aequalis ad basim cylindri AG, et ideo ad basim coni K. sit per 5. huius, sicut axis AX ad dimidium semidiametri GX: et ideo sicut celsitudo coni K, quae dupla est axis AX ad semidiametrum GX, quae dupla est sui dimidii, et ideo ad BD celsitudinem coni H. Propterea per 12.12. aequalis est conus H cono K, et ideo solido per triangulum BGZ descripto: quod est propositum.
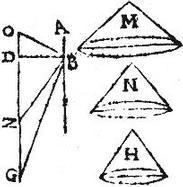
Hoc autem cum perpendicularis DB cadit inter puncta G, Z; quod si perpendicularis a puncto B ad GZ sit altera ipsarum BZ, BG demonstratio adhuc erit eadem, sed intra cylindrum AG unus describetur conus non duo. Si vero perpendicularis DB cadat extra puncta G, Z tunc [S:69] sic ostendam hanc propositionis partem, producta ZD ad libitum, ad signum O connectatur BO; sitque M conus basim habens aequam cylindricae superficiei, quam describit linea OG, celsitudo vero BD: item conus N basim habens aequalem cylindricae superficiei, quam describit linea OZ, et celsitudinem BD; eritque sicut dudum fuit demonstratum; conus M aequalis solido descripto per triangulum OBG: conus autem N aequalis solido descripto per triangulum OBZ; et quoniam cylindrica superficies, quam describit linea OG aequalis est cylindricis superficiebus simul sumptis, quas describunt lineae OZ, ZG. Ideo basis coni M aequalis est basibus conorum N, H, simul sumptis, quorum cum sit una celsitudo erit per antepraemissam. conus M aequalis conis N, H simul sumptis. Itaque de cono M conus N, et de solido per triangulum OBG descripto, solidum per triangulum OBZ descriptum, ab aequalibus scilicet aequalia, subtrahantur, et relinquitur conus H aequalis solido per triangulum BZG descripto: quod est propositum. Concluditur ergo quod solidum a triangulo lateraliter, vel angulariter axi in eodem plano existenti applicato, et circa eumdem axem perfecta revolutione circumducto descriptum, aequale est ei cono, cuius basis aequalis est conicae superficiei, vel cylindricae descriptae a latere trianguli, quod opponitur angulo applicato ad axem, celsitudo vero aequalis perpendiculari, quae a dicto angulo ad dictum latus egreditur ubicumque occurrat. Et haec est tota propositi summa, quae sequentibus inservit demonstrationibus.