PROPOSITIO XXI.
Conus, cuius basis aequalis est aggregato basium quotlibet conorum sub eodem fastigio, aequalis est aggregato omnium illorum.
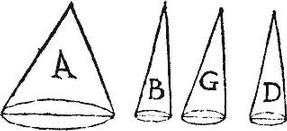
Exempli gratia basis coni A aequalis basibus simul sumptis aliquot conorum, utputa trium B, G, D: sitque omnium celsitudo una. Aio quod conus A aequalis est aggregato conorum B, G, D. Cum enim eorum altitudines sint aequales, erit per 11.12. conus B ad conum A, sicut basis coni B ad basim coni A. Item conus G ad conum A, sicut basis coni G ad basim coni A: quare per 24.5. coni B, G, simul sumpti ad conum A: sicut bases conorum B, G simul sumptae ad basim coni A. Adhuc conus D ad conum A, sicut basis coni D ad basim coni A. Rursum ergo per 24.5. coni B, G, D, simul sumpti ad conum A, sicut bases conorum B, G, D, simul sumptae ad basim coni A. Sed bases conorum B, G, D simul sumptae, per hypothesim, sunt aequales basi coni A: ergo et coni B, G, D simul sumpti sunt aequales cono A: quod est propositum. Idem demonstrabimus de quotcumque conis.
Idem concludere potes de cylindris, quorum celsitudines aequales.