F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis quadratura parabolae 5
<- App. -> <- = ->

PROPOSITIO V.

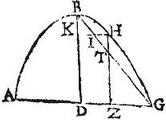
figura 5

Sit portio contenta a recta, et sectione rectanguli coni ABG, quae quidem BD penes diametrum sectans AG bifariam, vel ipsa diameter; et a puncto quolibet lineae AG, ut pote a puncto Z educatur penes BD ipsa ZH ad peripheriam, et producta occurrat ipsi GB productae ad signum T. Aio quod erit sicut GD ad DZ; sic ZT ad TH; agatur per H penes ipsam AG recta HK, secans BD apud K, et ipsam BG apud I, eritque per praemissam, sicut quadratum DG ad quadratum HK, vel DZ, sic DB ad BK; et ideo per 2. sexti Euclidis sic GB ad BI: sed per eandem, sicut quadratum GB ad quadratum BT, sic quadratum GD ad quadratum DZ. Ergo sicut GB ad BI, sic quadratum GB ad quadratum BT. Itaque dupla est ratio GB ad BI eius, quae GB ad BT. Quare ipsae GB, BT, BI, sunt continuae proportionales, coniunctim igitur (si Z signum cadit intra A, D; si vero intra signa D, G, eversim) erit sicut GT ad TI, sic GB ad BT; et ideo per 2. sexti Euclidis sic ut GD ad DZ; sed per eandem, sicut GT ad TI, sic ZT ad TH: ergo sicut GD ad DZ, sic ZT ad TH: quod est propositum.

Inizio della pagina
 ->