F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de momentis aequalibus Liber quartus 6
<- App. -> <- = ->

PROPOSITIO VI.

Omnis prismatis centrum est et ipsum centrum rectilinei, quod per aequalia secans solidum aequidistat basibus.

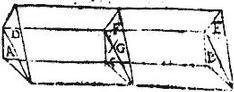
figura 9

Esto prisma ADBE, cuius bases aequidistantes quadrilaterae AD, BE; quibus aequidistet quadrilaterum CF secans solidum per medium. Demonstrandum est quod centrum prismatis ADBE est et centrum ipsum quadrilateri CF: secetur enim prisma ADBE in duo prismata triangularia AB, DE; quorum bases triangulae, et aequidistantes sint A, B, et D, E; quibus aequidistabunt triangula C, F, quae secant singula prismata per medium: eritque per 4. huius, centrum prismatis triangularis AB, centrum trianguli C, quod sit C punctum; et per eandem, centrum prismatis triangularis DE, centrum trianguli F, quod sit pun[S:161]ctum F: itaque coniuncta CF, erit per 6. primi momentorum aequalium; centrum totalis prismatis ADBE in ipsa recta CF; sit ipsum G. punctum: igitur per 27. primi momentorum aequalium, erit sicut prisma AB ad prisma DE: sic linea FG ad lineam GC: sed sicut est triangulum C ad triangulum F, sic est prisma AB ad prisma DE; (quandoquidem prismata sunt basibus proportionalia): ergo sicut linea FG ad lineam GC; sic triangulum C ad triangulum F. Quare per 28. primi momentorum aequalium, G centrum est quadrilateri CF: quod et centrum totalis prismatis ADBE fuit: sicut proponitur demonstrandum. Idem similiter demonstrabimus de prismate super basim pentagonam, hexagonam, aut plurium, et quotcumque laterum superficie erecto. Quod est propositum.

Inizio della pagina
 ->