F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de momentis aequalibus Liber quartus 1
<- App. -> <- = ->

PROPOSITIONES

Partim theoremata, et partim problemata.

PROPOSITIO PRIMA.

In sphaera centrum gravitatis est idem, quod magnitudinis.

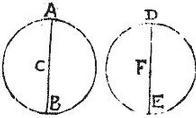
figura 1

Esto sphaera AB, cuius centrum gravitatis C punctum: aio quod C punctum est, et centrum magnitudinis sphaerae AB; sit enim ipsi AB sphaerae aequalis sphaera DE: cuius centrum gravitatis sit F, et coaptetur sphaera DE sphaerae AB, itaut ductis diametris AB, DE per puncta C, F, congruat in coaptatione diameter DE diametro AB: sic per 6. postulatum, congruet centrum F centro C, et perinde congruet linea DF lineae AC, et linea FE lineae CB. Rursum congruat sphaera DE sphaerae AB commutatis diametrorum extremis: nam rursus per 6. postulatum, congruent in coaptatione gravitatum centra: et ideo linea FD congruet lineae CB, et linea EF lineae AC: itaque cum in prima coaptatione linea DF congruat lineae AC: et in secunda coaptatione congruat lineae CB: iam aequales erunt lineae AC, CB: diameter autem est AB: ergo C punctum est centrum magnitudinis in sphera AB: quod erat demonstrandum.

Vel sic coaptentur sphaerae AB, DE; itaut in coaptatione secent se diametri AB, DE; congruent, autem per sextum postulatum, ipsa C, F gravitatum centra; et idcirco punctum F congruet puncto C. Quare diametri AB, DE, super ipso puncto C se invicem secabunt: diametri vero se vicissim secant centro; centrum igitur magnitudinis est punctum C in sphaera AB: quod erat demonstrandum.

Inizio della pagina
 ->