F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de momentis aequalibus Liber quartus 13
<- App. -> <- = ->

PROPOSITIO XIII.

Centrum gravitatis in pyramide triangulari est in linea, quae verticem cum centro basis coniungit, atque in eo lineae puncto, quod portionem ab basim suscipit, quae tertia pars est residuae.

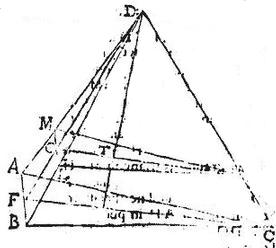
figura 22

Pyramis est ABCD super basim triangulam ABC, sitque trianguli ABC centrum V, et coniungatur DV, quae secetur apud T, ita ut DT tripla sit ipsius TV: demonstrandum est quod T punctum est centrum gravitatis pyramidis ABCD; ducatur per T punctum planum ipsi ABC basi aequidistans, et faciens triangulum LMH, et coniuncta CV: producatur, et coincidat ipsi AB apud F, et coniungatur FD secans LM apud G, et coniuncta GH: haec erit communis sectio triangulorum LMH, CDF; et quoniam DV linea est in plano trianguli CDF, ideo secabitur a linea GH in ipso plano trianguli LMH, hoc est in puncto T; et quoniam V centrum est trianguli ABC, ideo per 21. secundi aequalium momentorum, [S:169] linea AF aequalis est ipsi FB, cumque LM aequidistet ipsi AB; erit et MG aequalis GL. Item per 24. praecedentis, CV dupla est ipsius VF: sed aequidistat ipsi CF linea HG: igitur et HT dupla ipsius TG. Igitur per 25. eiusdem, T centrum est trianguli LMH: sed trianguli LMH planum sic secat ipsam DV, et perinde hypothemisas, ut portio ad basim sit tertia pars relictae ad verticem: ergo per praecedentem, T punctum, quod centrum est facti trianguli LMH est et centrum pyramidis ABCD. Quod fuit ostendendum.

Inizio della pagina
 ->