PROPOSITIO VI.

Quod duae praecedentes proponunt, aliter demonstrare.

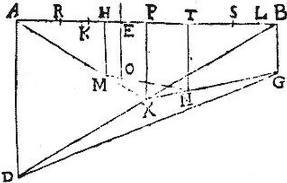
Neutra praecedentium indiget adminiculo alterius, hoc est utraque per se demonstrata est: potest igitur utraque ipsarum rursum demonstrari per reliquam indirecte: sic, in trapetio ABGD, cuius latera AD, BG aequidistent, alterum reliquum ut AB secetur in puncto E, sic ut AE ad EB sit sicut aggregatum ex duplo BG et ex AD ad aggregatum ex duplo AD et ex BG, et per punctum E ducatur ipsis AD, BG aequidistans EZ: demonstrandum est rursum, quod EZ incedit per centrum gravitatis trapetii ABG: nam sit centrum gravitatis, si possibile est extra lineam EZ in puncto O, et ducatur per punctum O ipsis AD, BG parallelus POQ: eritque per 5. praecedentem, AP ad PB, sicut congeries ex duplo BG, et ex AD ad congeriem ex duplo AD, et ex BG: sed sic est per hypothesim AE ad EB: igitur sicut AE ad EB, sic AP ad PB, et coniunctim sicut AB ad BE, sic iam AB ad BP: aequales ergo sunt EB, BP, totum et pars, quod est absurdum. Astruitur ergo propositum: sic ex 5. rursum demonstratur, quod 4. proponit.

Contra in eodem trapetio ducatur per centrum gravitatis linea EZ aequidistans ipsis AD, BG: demonstrandum rursus est, quod AE ad EB est sicut congeries ex duplo BG, et ex AD ad congeriem ex duplo AD et ex BG: namque si AE ad EB talem rationem non habeat; secetur AB in puncto P, itaut AP ad PB dictam servet rationem, et per punctum P ducatur PQ ipsis AD, BG aequidistans: ibitque per 4. huius, ipsa PQ per centrum gravitatis trapetii ABG: quod est impossibile: nam centrum ipsum fuit in linea EZ: astruitur ergo propositum, ut scilicet AE ad EB dictam habeant rationem: sic vicissim ex 4. praemissa, rursus demonstratur, quod quinta praecedens proposuerat.