F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de momentis aequalibus Liber tertius 2
<- App. -> <- = ->

PROPOSITIO II.

Quae trapetii latera aequidistantia bifariam secat, recta linea incedit per centrum gravitatis trapetii.

Trapetii ABGD latera AD, BG sint aequidistantia, quae singula bifariam secentur in punctis E, Z: aio quod coniuncta EZ recta incedit per centrum gravita[S:134]tis trapetii ABGD:

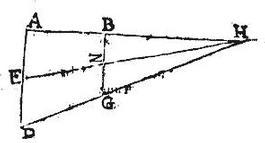
figura 2

coincidant enim reliqua AB, DG latera ad punctum H: eruntque per praecedentem, puncta E, Z, H in eadem recta linea : itaque EZ producta it per punctum H, eat, eritque per 22. praecedentis libelli, centrum trianguli AHD in linea EH, atque centrum trianguli BGH in linea ZH: itaque cum centrum totius trianguli AHD, et centrum partialis trianguli BGH sint in una recta, erit, et centrum reliquae partis scilicet trapetii ABGD in eadem recta EH: quandoquidem per 7. primi aequalium momentorum, recta per centrum unius partis, et per centrum totius ducta it per centrum reliquae partis: sed per ultimum postulatum, omnis figurae, cuius ambitus in eadem cava constiterit; centrum gravitatis intra figuram esse oportet: igitur centrum trapetii ABGD in linea EZ existet: sicut proponitur demonstrandum.

Inizio della pagina
 ->