PROPOSITIO XXXIV.
Datum rectilineum sic suspendere, ut assignatum in eo latus aequependeat.
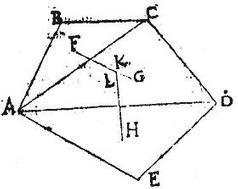
Sit exempli gratia datum pentagonum rectilineum ABCDE oportet ipsum ABCDE pentagonum ab aliquo puncto ita suspendere, ut datum in eo latus, quod sit AB aequependeat, hoc est aequidistet horizonti: comperiatur per praecedentem rectilinei ABCDE gravitatis centrum, quod sit L punctum; a quo ducatur ad datum latus AB perpendicularis linea LM quocumque feratur ad ambitum rectilinei. Dico itaque quod ABCDE rectilineum a puncto M suspensum sic pendet, ut AB aequidistet horizonti. Nam si rectilineum ABCDE libere pendeat a puncto M, iam per 2. praecedentis libri, centrum L erit in linea, quae a puncto M perpendicularis cadit ad horizontem: ergo ipsa LM perpendicularis erit ad horizontem; sed cum perpendicularis sit ad ipsam AB, iam aequidistabit AB horizonti, et ideo per deffinitionem aequependebit.
Vel sic collocetur rectilineum ABC in tali situ, ut LM perpendicularis sit ad horizontem, et suspendatur a puncto M. Nam per 3. praecedentis libri, sic pendebit ut locatum est, ipsa scilicet ML perpendiculari existente ad horizontem; et ideo sicut prius, suspenso rectilineo a puncto M aequependebit latus AB: quod quidem proponebatur faciendum.