F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de momentis aequalibus Liber secundus 22
<- App. -> <- = ->

PROPOSITIO XXII.

Si trianguli cuiuslibet latus quodvis per aequalia secetur, quae a sectionis puncto ad oppositum angulum linea ducitur, per centrum gravitatis trianguli transit.

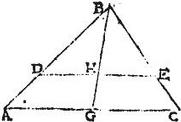
figura 25

In triangulo ABC latus quodlibet ut AC per medium secetur in puncto G, et ducatur BG: aio quod BG transit per centrum trianguli ABC: nam si BG per centrum non it, eat si possibile est, per centrum KB incidens lateri AC apud K punctum; et secabitur AC apud K per aequalia per praecedentem, secatur, et per aequalia apud G, per hypothesim: quod est impossibile: astruitur ergo propositum,

Alia demonstratio, qua utitur Archimedes.

figura 26

In triangulo rectilineo ABC quodvis latus ut puta AC secetur per aequalia in puncto D, et ducatur BD linea: ostendendum est quod centrum trianguli ABC est in linea BD, secus sit, si possibile est, centrum extra lineam BD ut puta in puncto E, et ipsi BD paralleli agantur EG, AH, sitque sicut AD ad DG, sic iam triangulum ABC ad superficiem L: mox ductis intra triangulum ABC lineis ipsi AC basi aequidistantibus, et per earum extrema aliis ipsi BD aequidistantibus: donec facta scalatim parallelogramma relinquant spatia trigona lateralia, quod aggregatum sit minus superficie L. Erit iam maior ratio trianguli ABC ad dictum aggregatum, quam triangulum ABC ad superficiem L, hoc est quam lineae AD ad lineam DG; cunque centrum commune dictorum parallelogrammorum per 3. secundi, et per 6. primi erit in linea BD, sit illud punctum F, et coniungatur, ac producatur FEH in indefinitum: eritque propter aequidistantiam linearum sicut AD ad DG, sic iam HF ad FE: maior ergo erit ratio trianguli ABC ad aggregatum dictorum lateralium trigonorum, quam ratio lineae HF ad lineam FE: ponatur itaque sicut triangulum ABC ad dictum aggregatum relictorum lateralium trigonorum, sic iam linea KF ad lineam FE: eritque disiunctim sicut linea KE ad lineam EF, sic iam congeries factorum parallelogrammorum ad dictum aggregatum relictorum trigonorum: cumque E sit centrum totius trianguli ABC, atque punctum F centrum partis unius, [S:126] scilicet congeriei factorum parallelogrammorum: erit per 28. primi, K centrum reliquae partis, scilicet aggregati relictorum trigonorum: quod est impossibile per ultimum postulatum; non enim possibile est centrum sit extra ipsius gravis ambitum: constat ergo propositum.

Inizio della pagina
 ->