F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de momentis aequalibus Liber primus 48
<- App. -> <- = ->

PROPOSITIO XXXXVIII.

Si fuerint tres magnitudines, et quae ratio est excessus secundae super primam ad primam, ea sit ratio excessus tertiae super primam ad aggregatum ex prima, et secunda; continue proportionales erunt magnitudines.

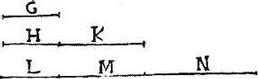
figura 45

Haec est conversa 42. huius. Sunto tres magnitudines G, HK, LMN, ita ut G, H, L sint inter se aequales, et K, M aequales: unde K erit differentia primae, et secundae, MN differentia primae, et tertiae; sitque sicut K ad G, sic MN ad GHK: aio quod tres magnitudines G, HK, LMN sunt continue proportionales; hoc est, sicut G prima ad HK secundam, sic HK secunda ad LMN tertiam. Cum enim per hypothesim sit sicut MN totum ad GHK totum, sic M ablatum, ad G ablatum erit per 19.5. et sic N reliquum ad HK reliquum: et coniunctim, sicut KG, ad G, sic NHK ad HK, hoc est sicut KH ad G sic LNM ad HK: itaque conversim sicut G ad HK, sic HK ad LMN: quod est propositum.

Inizio della pagina
 ->