F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de momentis aequalibus Liber primus 43
<- App. -> <- = ->

PROPOSITIO XXXXIII.

Crementa momentorum sunt proportionalia crementis spatiorum.

Sit libra ACB, in qua punctum appensionis sit C; grave autem D primum a puncto A suspensum, hoc est ad spatium AC aequeponderet primum gravi B: deinde a puncto F ad spatium scilicet FC aequiponderet gravi BE: adhuc a puncto H ad spatium HC aequiponderet gravi BEG: dico iam quod crementa momentorum a gravi D ad ea spatia factorum sunt spatiis ipsis proportionalia: nam cum per hypothesim, momentum gravis D ad spatium CA pendentis factum sit aequale momento gravis B: cumque momentum gravis D ad spatium CF suspensi factum sit aequale momento gravis BE: cum denique momentum gravis D ad spatium CH ponderantis factum sit aequale momento gravis BEG: et per 37. huius, ipsa momenta B, BE, BEG [S:107] sint proportionalia gravibus ipsis B, BE, BEG: et crementa crementis: demonstrandum est quod crementa horum gravium, quae sunt E, G sunt proportionalia crementis spatiorum, quae sunt AF, FH.

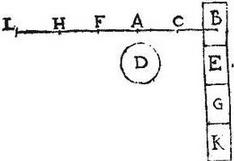
figura 40

Itaque quoniam per 38. huius, momenta gravis D ad inaequalia spatia CA, CF, CH pendentis facta sunt proportionalia spatiis ipsis: ideo et momenta B, BE, BEG praedictis momentis gravis D singula singulis aequalia, iisdem spatiis CA, CF, CH erunt proportionalia: hoc est sicut spatium AC ad spatium CF, sic momentum ipsum B ad momentum BE; et conversim sicut spatium FC ad spatium CA; sic momentum BE ad momentum B: et conversim sicut spatium CF ad spatium FA, sic momentum BE ad momentum E. Et similiter ostendam quod sicut spatium CH ad HF, sic momentum BEG ad momentum G: et disiunctim sicut spatium CF ad spatium FH, sic momentum BE ad momentum G, et conversim, sicut spatium HF ad spatium FC, sic momentum G ad momentum BE; fuit autem sicut spatium CF ad spatium FA, sic momentum BE ad momentum E: igitur ex aequali sicut spatium HF ad spatium FA, sic momentum G ad momentum E: quod erat iam demonstrandum.

COROLLARIUM.

Unde iam manifeste constat, quod si crementa spatiorum fuerint aequalia, et crementa momentorum erunt etiam inter se aequalia, et e contrario.

Similiter autem ostendam, quod sicut spatium LH ad FH, sic et momentum K ad momentum G; et de quocunque deinceps spatiorum crementis, atque momentorum.

Inizio della pagina
 ->