PROPOSITIO IX.
Si centra quotcumque gravium sint in uno plano; centrum aggregati ex illis tanquam unius erit in eodem plano.
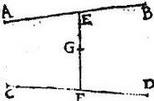
Ut si quatuor gravium centra A, B, C, D, sint in eodem plano: dico quod centrum aggregati ex his erit in eodem plano: coniungantur enim AB, CD: eruntque per 6. huius. centrum totius AB in recta AB quod sit E: centrum totius CD in recta CD quod sit F: coniungatur item EF, eritque per 6. centrum aggregati ex A, B, C, D, in recta EF quod sit G; cumque AB, CD rectae sint, per hypothesim, in uno plano, erit et EF in eodem plano; et pun[S:91]ctum G similiter in eodem: atque id idem ostendemus de quotcunque gravibus, quorum centra in eodem plano locata sint; sicut proponitur demonstrandum.