PROPOSITIO III.
Plano quopiam solidum conoides tangente, si planum aliud per axem solidi, perque punctum contactus ducatur, id rectum erit super tangente plano.
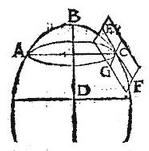
Solidum conoides ABC. cuius axis BD. tangatur a plano quopiam, fiet autem contactus in puncto per praecedentem: quod punctum sit C; ducatur per axem BD, perque punctum C planum ABC. Aio quod planum ABC rectum est ad ipsum tangens planum. Sit enim plani ABC, quod per axem, planique tangentis apud C communis sectio recta linea ECF. Item per punctum contactus C ducatur planum rectum ad axem BD, eritque per 17. praemissi, facta sectio, circulus AC, cuius diameter AC, sit autem huius plani cum plano tangente communis sectio recta CG, quae utique cum sit in plano tangente cadet extra superficiem solidi, et perinde extra circulum AC in tali superficie existentem. Igitur CG recta tangit circulum AC apud C extremum diametrum; perpendicularis est igitur GC linea super AC lineam. Sed AC linea communis sectio est circuli cum plano ABC: ergo GC perpendicularis est super planum ABC: quare planum tangens EGF in quo ipsa GC per 18. undecimi Euclidis, rectum erit plano ABC per axim BD, tactumque C ducto. Quod erat demonstrandum.