ARCHIMEDIS
DE CONOIDIBUS, ET SPHAEROIDIBUS
FIGURIS INVENTORUM.
EX TRADITIONE
MAUROLICI
PROPOSITIO I.
Si in superficie cuiuslibet solidi conoidibus duo puncta, utcumque signentur; linea recta, quae puncta connectit, intra solidi superficiem cadit.
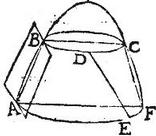
Esto solidum conoides ABC, in cuius superficie signentur duo puncta, ut puta A, B. Aio quod AB, recta cadit intra superficiem solidi: ducatur enim planum per A, B puncta secans solidum; et si facta sectio sit aliqua ex conicis sectionibus ut ostensum fuit in praemisso libello: iam tunc recta linea AB, per decimam primi conicorum elementorum cadet intra peripheriam sectionis, et perinde intra superficiem solidi, sint autem et puncta D, E, quae non sint in aliqua peripheria sectionis conicae; et ducatur DE recta. Aio quod etiam DE recta intra superficiem solidi cadet. Ducantur enim per D, E puncta plana aequidistantia ad axim solidi erecta: eruntque per 17. praemissi, factae sectiones circuli qui sint AEF; BDC. Secetur et solidum plano per axem, eritque per 16. praemissi, facta sectio ipsa, quae solidum describit. Esto ABC. Et ducatur recta AB; quae ut ostensum est intra sectionem cadit; itaque in circulatione sectionis ABC, describentes solidum recta AB, circulata conicam superficiem quae intra solidi superficiem est, describit. Verum recta linea DE. per 2. primi conicorum elementorum cadit intra talem superficiem conicam: et multo magis intra superficiem solidi cadet. Quod erat demonstrandum.