PROPOSITIO VII.

Ellipsis ad circulum super maiorem suam diametrum descriptum est sicut minor diameter ad maiorem.

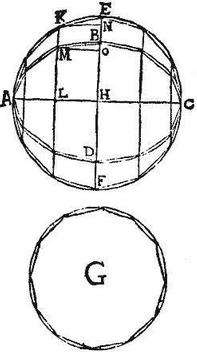
Ellipsis esto ABCD super cuius maiorem diametrum AC. Descriptus sit circulus EF. Dico iam quod area ellipsis BD ad aream circuli EF est sicut BD minor ellipsis diameter ad EF circuli diametrum. Sit enim sicut linea BD ad lineam EF, sic circulus G ad circulum EF: erit circulus G aequalis ellipsi BD. Secus enim sit circulus G maior, quam ellipsis BD, et inscribatur circulo G multiangula figura maior ellipsi BD; et ei similis inscribatur circulo EF. Et ductis aequidistantibus ipsi EF, ductisque inter eas chordis in BD ellipsi figura totidem laterum describatur; eritque figura BD ad figuram EF sicut linea BD, ad lineam EF (quoniam scilicet [S:232] trapetia finiuntur basibus superis, et inferis proportionalibus: et perinde habent linearum correlativarum proportionem; et ideo cuncta trapezia ad cuncta trapezia, hoc est figura ad figuram, sicut tota linea ad totam lineam:) igitur sicut figura BD ad figuram EF, sic circulus G ad circulum EF, et sicut figura G ad figuram EF; ergo sicut figura G ad figuram EF, sic figura BD ad figuram EF: itaque aequalis est figura G figurae BD; et ideo figura G est minor ellipsi BD; fuit autem maior, quod est absurdum. Non est ergo circulus G maior ellipsi BD. Sit deinde minor circulus G, quam ellipsis BD; et inscribatur ellipsi BD multiangula figura BD maior circulo G: et inter easdem aequidistantes figura totidem laterum inscribatur circulo EF, et ei similis circulo G; eritque rursum figura EF ad figuram BD, sicut linea EF ad lineam BD: sed sic fuit iam prius circulus EF ad circulum G, atque sic est ipsa figura EF ad figuram G. Igitur figura EF ad figuram G est sicut figura EF ad figuram BD. Quare figura G aequalis figurae BD, et perinde figura BD minor circulo G, fuitque maior, quod est absurdum. Non est igitur minor circulus G ellipsi BD, sed nec maior fuit: super est ergo, ut sit aequalis: sicut fuerat demonstrandum.