PROPOSITIO VIII

82 Si in sphaera circulus, qui per eius centrum non transeat, signetur, et a centro sphaerae ad centrum circuli recta linea ducatur, necesse est eam super circuli signati superficiem esse perpendicularem.

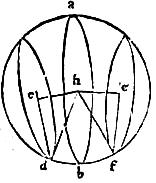
In sphaera abcd, cuius centrum h, signetur circulus, cuius centrum g, et coniungatur linea recta gh: aio quod gh perpendicularis est circulo, cuius centrum g. 83 Et haec propositio est conversa secundae partis corollarii primae huius. 84 Ducam duas diametros circuli signati bd ef quascunque sese in centro g invicem secantes et coniungam rectas hb hd he hf. 85 Eruntque, per diffinitiones sphaerae et circuli, quatuor triangula hgb hgd hge hgf inter se aequalium laterum et ideo, per 8 primi Euclidis, aequalium angulorum, quam ob rem anguli eorum apud g constituti aequales, unde per diffinitionem lineae perpendicularis [S:2v] super lineam, ipsa linea hg perpendicularis erit tam diametro bd quam diametro ef et idcirco, per 4 undecimi, eadem hg perpendicularis erit plano circuli, in quo diametri praedicti iacent. 86 Quod etiam et indirecte ostendi posset per corollarium primae vel per corollarium secundae huius. 87 Itaque pluribus viis constat quod proponitur demonstrandum.