PROPOSITIO XXVII
190 Omnis circulus, a cuius polo recta linea ad ipsius periferiam ducta est aequalis lateri quadrati maiori circulo in sphaera signato inscripti, est circulus8 maior.
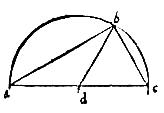
191 Sit circulus in sphaera signatus abc, a cuius polo d linea da ducta ad eius periferiam ponatur esse latus quadrati inscripti circulo maiori in eadem sphaera signato9: [S:4v] aio tunc quod circulus abc maior est. 192 Nam ducam planum per lineam ad perque centrum10 ipsius sphaerae sitque communis sectio plani producti et sphaerae circulus ade per primam huius, qui per 6 circulus maior erit; communis autem sectio plani cum circulo abc sit linea recta ac. 193 Deinde ducam rectam dc, quae ex diffinitione poli erit qualis rectae ad. 194 Est autem per hypothesim ad latus quadrati inscripti circulo adc maiori: ergo et recta dc latus alterum dicti quadrati. 195 Quare ipsi arcus ad dc sunt quadrantes circuli adc et ideo adc semicirculus. 196 Sed per 20 huius, circulus adc secat ipsum abc circulum per aequalia quia maior et per eius polos. 197 Igitur per 17 huius circulus abc maior est, quod est propositum.