PROPOSITIO XVII
132 Omnes circuli in sphaera se invicem per aequalia dividentes sunt maiores.
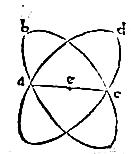
133 In eadem descriptione circuli abc adc in sphaera designati dividant se in semicirculos invicem: aio quod maiores sunt. 134 Nam si per aequa se vicissim dispescunt, communis earum sectio ac diameter erit utriusque; igitur centrum commune eorum erit in ac diametro. 135 Sit illud punctum e, per quod agantur rectae ef eg singulae singulis circulis perpendiculares, quae per corollarium 2 huius transibunt per centrum sphaer<a>e. 136 Itaque centrum sphaer<a>e esse non poterit alibi quam in puncto e in quo perpendiculares se mutuo secant. 137 Ergo per sextam huius uterque circulorum abc adc maior est, sicut proponitur demonstrandum.