PROPOSITIO XXXI

225 In triangulo rectangulo ex arcubus circulorum maiorum in superficie sphaerae constituto, sinus totus ad sinum arcus unum ex acutis angulis subtendentis est sicut quadratum gnomonis ad rectangulum comprehensum sub umbris versis, quarum una complemento reliqui acuti, altera vero arcui eundem acutum subtendenti debetur.

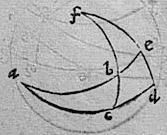
226 Repetita descriptione 27 huius, in triangulo abc demonstrandum est quod sinus totus ad sinum arcus ca subtendentis angulum acutum abc est sicut quadratum gnomonis ad rectangulum quod fit ex duabus umbris versis, quarum una debetur arcui fe quod complementum est anguli bac, altera respondet arcui bc subtendenti reliquum acutum angulum bac. Quod sic ostenditur. 227 Per praecedentem, sicut gnomo ad umbram versam arcus fe sic sinus arcus de ad sinum arcus ef et rursum per eandem sicut gnomo ad umbram versam arcus bc sic sinus [S:59r] arcus fb sinum arcus bc. 228 Sed per 24^m 6 Elementorum Euclidis, ratio quadrati gnomonis ad quadrangulum ex umbris versis arcuum fe bc componitur ex rationibus duabus, videlicet gnomonis ad umbram versam arcus fe et gnomonis ad umbram versam arcus bc. 229 Quare et eadem ratio componetur ex rationibus duabus, quae sunt praedictis aequales, scilicet sinus arcus de ad sinum arcus ef et sinus arcus fb ad sinum⁴⁷ arcus bc. 230 Per 4^m vel 5^m huius, ex iisdem rationibus duabus scilicet sinus arcus de ad sinum arcus ef et sinus arcus fb ad sinum arcus bc componitur ratio sinus arcus da ad sinum arcus ac. 231 Igitur ex aequa proportione, erit sinus arcus da hoc est sinus totus ad sinum arcus ac iam sicut quadratum gnomonis ad rectangulum contentum sub umbris versis arcuum fe bc. Et id proponebatur demonstrandum.

COROLLARIA

232 Hinc manifestum est quod si in duobus triangulis sphaeralibus orthogoniis duo latera quae circum rectos angulos aequalia fuerint: tunc rectangula, quae ex umbris versis reliquorum laterum, quae circum rectos, in umbras versas debitas complementis subtensorum angulorum producuntur, erunt et invicem aequalia. Et contrario.