PROPOSITIO XXVIIII

206 In omni triangulo ex arcubus circulorum maiorum in superficie sphaerae constituto, sinus versus anguli cuiuslibet ad differentiam duorum sinuum versorum, quorum unus est lateris eum angulum subtendentis, alter vero differentiae duorum arcuum ipsum angulum continentium, est sicut quadratum sinus totius ad id quod sub sinibus arcuum eorundem continetur rectangulum.

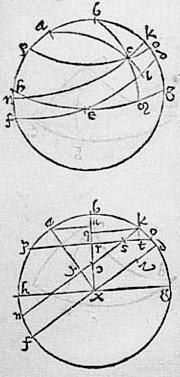
207 Sit in superficie sphaerae ex arcubus circulorum maiorum constructum utcumque triangulum abc. Completoque circulo abd super polis a b circuli describantur, maiores quidem def geh [S:58v] minores vero kcn ocp, item quadrantes circulorum maiorum a polis ad circulos maiores acl bcm. 208 Rursum in alia descriptione (confusionis tollendae gratia) describantur horum circulorum diametri, axes, sinusque. Ac primum descripto, ut iacet, circulo abd describantur aliorum diametri, quae sunt communes eorum cum abd circuli plano sectiones, hoc pacto. 209 Punctum x sit centrum sphaerae et circulorum maiorum, recta dxf diameter circuli def, recta gxh diameter circuli geh, recta kyn diameter circuli kcn, recta orp diameter circuli ocp se invicem secantes in puncto s, item rectae xb xa axes ipsorum geh def circulorum sive semidiametri circulorum bcm acl, adhuc lineae au kq perpendiculares ad xb, linea kt perpendicularis ad os. 210 Quibus pactis patet quod linea au est sinus rectus arcus ab, linea ky est sinus rectus arcus ak et etiam arcus ac (quandoquidem aequales sunt, quoniam a polo ad periferiam circuli kcn), linea or sinus arcus bo et ei aequalis arcus bc (quoniam a polo ad periferiam circuli ocp), linea kq sinus arcus bk qui est differentia arcuum ak ab. 211 Unde et linea br erit sinus versus arcus bo sive bc, linea bq sinus versus arcus bk differentiae praedictae, linea qr differentia talium sinuum versorum, linea ks sinus versus arcus kc. Quae omnia patent per primam praecedentis libelli. 212 Ponatur itaque recta dz sinus versus arcus⁴⁶ dl sive anguli bac, constabitque demonstrandum esse quod dz sinus versus anguli bac ad rq differentiam sinuum versorum arcubus bc bk debitorum est sicut quadratum sinus totius, quod fit ex dx in xa ad rectangulum quod fit ex au ky qui scilicet sunt sinus recti arcuum ab ac hoc modo. 213 Quoniam per 14^m secundi Sphaericorum Elementorum, arcus dl kc sunt similes, et in similibus arcubus sinus sunt semidiametris proportionales. Et ideo sicut linea dz ad lineam ks sic linea dx ad lineam ky. 214 Item quoniam aequiangulum est triangulum kts triangulo jrs, et triangulum jrs triangulo jyx, et triangulum jyx triangulo aux, ideo triangula kts aux aequiangula sunt. 215 Quare per 4^m sexti Euclidis, linea xa ad lineam au sicut linea sk ad kt. Verum posita linea ks media, ratio dz ad kt vel qr componitur ex rationibus dz ad ks et ks ad kt et ideo ex rationibus dx ad ky et xa ad au quae sunt illis eaedem. 216 Per 24^m sexti Elementorum Euclidis, ratio quadrati sinus totius quod fit ex dx xa ad quadrangulum quod fit ex au ky componitur ex rationibus dx ad ky et xa ad au iisdem. 217 Igitur ex aequa proportione, erit linea dz ad qr sicut quadratum sinus totius ad rectangulum au ky quandoquidem proponebatur demonstrandum.