PROPOSITIO XXII
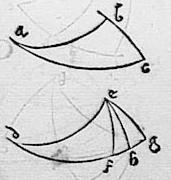
160 Si fuerint in superficie sphaerae duo triangula ex arcubus circulorum maiorum quorum unius angulus acutus aequalis alterius angulo acuto et alius unius angulus cum alio alterius angulo iunctus conficiat duos rectos: tunc sinus arcuum his angulis oppositorum erunt sinibus arcuum oppositorum acutis proportionales.
161 Sint in superficie sphaerae duo triangula abc def ex arcubus circulorum maiorum, in quibus anguli a d acuti sint invicem aequales, angulus autem c cum angulo efd iunctus conficiat duos rectos: aio quod sinus arcus ab ad sinum arcus de est sicut sinus arcus bc ad sinum arcus ef. 162 Nam si anguli c f sint recti, constat propositum per 7m praemissi libelli. 163 Secus autem talium angulorum alter erit acutus, alter obtusus, quandoquidem coniuncti duos rectos conficiunt. 164 Acutus esto angulus c, obtusus vero efd, et producto arcu df ad usque g, perpendicularis ad ipsum circuli maioris arcus ducatur eh, ipsique fh aequalis arcus ponatur hg et arcus circuli maioris ducatur eg, eruntque per 28m secundi Sphaericorum Elementorum, arcus fe eg aequales. 165 Sicut arcus eh communis triangulis feh geh rectangulis, ergo per 8m praemissi, anguli efh egh aequales. Angulus autem efh cum angulo efd conficit duos rectos atque angulus c cum angulo efd conficit duos rectos. 166 Quare dempto communi angulo efd superest angulus efh aequalis angulo c, et ideo angulus egh aequalis angulo c. 167 Supponuntur autem et anguli a d aequales, igitur per 11m praemissi, sinus arcus ab ad sinum arcus de sicut sinus arcus bc ad sinum arcus eg, aequalis autem fuit arcus eg arcui ef. Itaque et sinus arcus ab ad sinum arcus de sicut sinus arcus bc ad sinum arcus ef. Quod fuit demonstrandum.