PROPOSITIO XXXVIIII

242 Quod si in eodem lineamento, sinus totus ad sinum secundum alterius perpendicularium arcuum maior sit quam sinus secundus alterius perpendicularis sinum secundum anguli acuti perpendicularibus oppositi: tunc arcus inter casus perpendicularium maior erit arcu inter signata puncta cadente et arcus ad angulum maiores erunt singuli singulis coalternis; et angulorum a perpendicularibus ad puncta signata factorum sinus maiores erunt, alter alterius perpendicularis sinu secundo. [S:51v]

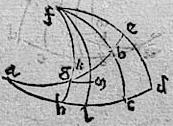
243 In eadem descriptione ponatur ratio sinus totius ad sinum fk maior, quam ratio sinus bf ad sinum fe: aio tunc quod producto quadrante circuli maioris fkl arcus cl maior erit arcu bk, item arcus ak maior arcu cd et arcus al maior arcu be, atque sinus anguli akl maior sinu arcus fb, et sinus anguli abc maior sinu arcus fk. Quod sic patet. 244 Quoniam maior est sinus totus ad sinum arcus⁵⁵ fk quam sinus arcus bf ad sinum arcus fe. Ponatur iam sicut sinus arcus bf ad sinum arcus fe sic sinus totus ad sinum arcus fm. 245 Sic maior erit arcus fm arcu fk. Describatur super f polo parallelus ipsi ad, circulus mg incidens circulo ae apud g punctum. Eritque per diffinitionem poli aequalis fg arcus ipsi fm arcui. 246 Quare, producto fgh quadrante, erit sicut sinus totus ad sinum arcusfg sic sinus arcus bf ad sinum arcus fe. Et ideo per 15^m sexti Euclidis, quadrangulum quod ex sinu toto sinuque arcus fe aequale erit quadrangulo quod ex sinibus arcuum fg fb. 247 Igitur quadrangulum quod ex sinu toto sinuque arcus fe maius erit quadrangulo quod ex sinibus arcuum fk fb (quandoquidem minor est fk arcu fg). Verum per 34^m huius, sicut quadrangulum quod ex sinu toto sinuque arcus fe ad quadrangulum quod ex sinibus arcuum fk fb sic est iam sinus arcus cl ad sinum arcus bk. 248 Ergo maior sinus arcus cl sinu arcus bk et perinde maior arcus cl arcu bk.

249 Et quoniam per 35^m huius, arcus ag aequalis arcui cd et arcus ah aequalis arcui be, propterea iam, arcus ak maior erit arcu cd et arcus al maior arcu be. Et quoniam per 6^m huius, sicut sinus arcus gf ad sinum arcus fe sic sinus totus ad sinum anguli agh, et sicut sinus arcus kf ad sinum arcus fe sic sinus⁵⁶ totus ad sinum anguli akl. 250 Estque maior sinus arcus gf ad sinum arcus fe quam sinus arcus kf ad sinum arcus fe. Ideo maior erit sinus totus ad sinum anguli agh quam ad sinum anguli akl. Et ob id maior erit sinus anguli akl sinu anguli agh et angulus angulo. 251 Sed per 35^m huius, sinus anguli agh aequalis est sinui arcus fb, igitur sinus anguli akl maior sinu arcus fb. Et quoniam per 35^m eandem, sinus anguli abc aequalis est sinui arcus fg. Arcus autem fg maior arcu fk et sinus sinu. Ideo sinus idem anguli abc maior erit sinu arcus fk. Constat ergo quidquid proponebatur demonstrandum.