PROPOSITIO XVIIII
129 Si in triangulo ex arcubus circulorum maiorum quadrante minoribus in superficie sphaerae, sinus secundus primi arcus ad sinum secundum secundi arcus sit, sicut sinus totus ad sinum secundum tertii arcus: tunc angulus secundo lateri oppositus rectus erit.
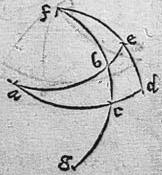
130 Sit in superficie sphaerae triangulum abc ex arcubus circulorum maiorum, qui singuli sint quadrante inferiores atque sinus secundus arcus bc ad sinum secundum arcus ab sit sicut sinus totus ad sinum secundum arcus ac: aio quod qui ad c angulus rectus erit. 131 Producantur enim arcus ab ac et ponatur quadrantes ae ad et ducatur arcus circuli maioris de qui productus coincidat arcui cb producto apud f. Eruntque per 3m huius, qui ad d e anguli recti. Quare per 7m huius, sinus arcus fb ad sinum arcus fc erit sicut sinus arcus be ad sinum arcus cd hoc est sicut sinus secundus 2s arcus ab ad sinum secundum arcus ac. 132 Producatur arcus bc et ponatur quadrans bg. Eritque per hypothesim et permutatam proportionem, sinus arcus cg (qui videlicet est sinus secundus arcus bc ) ad sinum arcus bg (qui est sinus totus) sicut sinus arcus be ad sinum arcus cd. Et perinde sicut sinus arcus fb ad sinum arcus fc. Duo arcus igitur fb fc et totidem cg bg ex eodem circulo sumpti communemque excessum24 bc habentes sortiuntur sinus proportionales. 133 Ergo per praecedentem,huiusmodi arcus erunt singuli singulis aequales, hoc est maior maiori et minor minori, aequalis ergo erit arcus fc arcui bg. 134 Quadrans autem fuit bg et quadrans igitur erit fc sicut qui ad d angulus rectus. Igitur et qui ad c angulus per 4m huius, rectus erit. Quod fuit demonstrandum.