11⁶

Ratio sexcupla superpartiens tres quartas, dupla est ad rationem, quam habet octahedri solidum ad pyramidis solidum in eadem sphaera existentium.

Eductis a centro sphaerae ad angulos solidorum rectis, secetur octahedrum in octo pyramides. Tetrahedrum vero seu pyramis in quatuor. Eruntque octo pyramidum celsitudines ipsae perpendiculares a centro sphaerae ad bases octahedri. 14 Quatuor vero pyramidum celsitudines ipsae perpendiculares ab eodem centro ad bases tetrahedri. Sit itaque pyramis a cuius basis sit superficiei octahedri aequalis, celsitudo vero aequalis perpendiculari octahedri. Sit item b pyramis, cuius basis superficiei tetrahedri, celsitudo vero perpendiculari tetrahedri sit aequalis. Eritque per 6^am Undecimi, pyramis a octahedro, pyramis vero b tetrahedro aequalis.

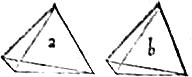
15 Quibus suppositis, erit per 7^am huius, celsitudo pyramidis a ad celsitudinem pyramidis b potentialiter tripla. Et ideo sicut 27 ad 9 basis vero pyramidis a ad basim pyramidis b per corollarium praecedentis erit sesquialtera. Et ideo potentialiter, sicut 9 ad 4. 16 Ergo per aequam proportionem, ratio pyramidis a ad pyramidem b (quae ex rationibus celsitudinum et basium componitur) duplicata erit, sicut 27 ad 4 sicut enim simplae simplam, sic duplae duplam rationem componunt. Igitur et eadem ratio octahedri ad tetrahedrum, sicut proponitur demonstrandum.