// PROPOSITIONES, QUARUM QUAEDAM SUNT problemata, quaedam theo- remata.

1^a Si hyperbolen ad summitatem linea tangat: et ex ipsa in utramque² diametri relicta sit aequalis potenti quadrantem speciei, et a centro sectionis ad relictos terminos tangentis ducantur lineae, productae nequaquam coincident sectioni.

Sit hyperbole, cuius diameter ab. // Centrum g. // Recta bz. // Tangens de. // Punctum tactus b. // Et tam db quam be possit quartam partem speciei, quae scilicet sub ab bz³. // Et coniungantur dg ge et producantur versus sectionem quantumlibet.

// Dico⁴ gd ge nusquam coincident [A:39r]sectioni.

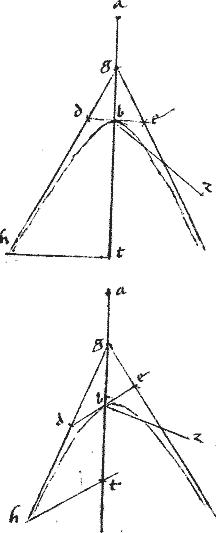
// Coincidat⁵ enim, si possibile est, ut gd apud h. // Et ordinate applicaretur ht quae, per additam post 32^am praecedentis libelli, aequidistabit ipsi de tangenti. // Et quoniam per primam 6ⁱ Euclidis ab bz sic ab abz et ab abz sicut gb bd quandoquidem tam gb ipsius ab quam db ipsius abz quadrans est.

Ideo et⁶ gb bd sicut abbz.

Sed, propter gbd gth⁷ similitudinem gb bd sicut⁸ gt th.

Et⁹ per 12^am praecedentis libri, sicut abbz sic atb th.

Igitur gt atb tum th eadem ratio .

Quare per 9^am quinti Euclidis, atb aequale est gt.

Et ideo per 16^am sexti bttgta sunt in proportione continua.

Eritque ta totum gt totum, sicut gt abscisum tb abscisum¹⁰.

Unde, per 19^am 5ⁱ Euclidis ag reliquum¹¹ bg reliquum sicut ta totum gt totum. Maius autem¹² ta quam gt. Ergo et ag maior, quam gb. Sed supponuntur aequalia: quod est absurdum. Non igitur gd et simili ratione ge coincidet sectioni. Quod erat demonstrandum.

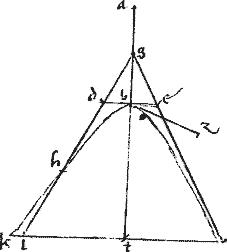
Idem et aliter ostendam. // Coincidat enim, si possibile est, gd producta sectioni apud h. // Et quoniam bg non minor est dimidio ipsius ab. Ideo, per 29^am primi Conicorum gh producta intra sectionem cadet. // Cadat, sitque ghl periferia vero sectionis sit ghk¹³. // Et applicetur ordinate klt quae, per additam post 32^am praemissi libri, erit penes de quandoquidem ordinata est et¹⁴ de.

// Et, quoniam, per primam 6ⁱ Euclidis sicut ab bz sic ab abz. Et ab abz sicut bg db [A:39v]quandoquidem, tam bg ^ti ab quam db ipsius ^li abz quadrans est.

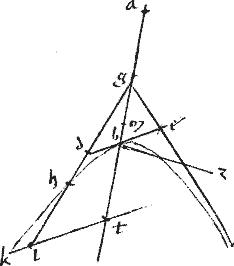
Ideo gb bd sicut ab bz.

// Sed propter gbd gtl similitudinem, sicut gb bd sic gt tl.

Ergo et¹⁵ gt tl sicut ab bz.

Sit¹⁶ autem, sicut at tg sic ag gm. Cumque sit at maior quam tg erit et ag maior, quam gm.

Et, per 19^am quinti erit, sicut totum at¹⁷ totum tg sic reliquum gt reliquum tm. // Hoc est at tg tm erunt continuae proportionales.

// Quare per 16^am sexti Euclidis atm aequalis¹⁸ erit tg. Et ideo gt maius^{19 lo} atb. Et per 8^am 5ⁱ Euclidis gt tk maius²⁰, quam atb tk.

// Sed per 12^am primi Conicorum atb tk sicut ab bz. Ergo gt tk maius²¹, quam ab bz.

// Fuit autem ab bz sicut gt tl. Igitur gt tk maius²² quam gt tl²³.

// Quare, per 10^am quinti Euclidis tl maius tk. Et ideo tl maior quam tk pars toto, quod est absurdum.

// Non igitur gd et similibus argumentis, neque ge coincidet sectioni: quod erat demonstrandum.

Vocentur autem ipsae gd ge non tangentes²⁴, sive non coincidentes: quippe quae etiam si in infinitum producantur, numquam sectioni, coincidunt.

Per summitatem hyperboles penes alteram non tangentium acta linea non alibi, quam in summitate ipsa coincidit sectioni, productaque sub eo puncto semper intra sectionem cadit²⁵.

Iis stantibus, quae in praemissa sunt adducta: ducatur penes ipsam bg non tangentem linea bk.

// Dico iam quod bk non alibi quam in puncto b summitatis sectioni coincidet²⁶, inferiusque producta semper intra sectionem deducitur. // Coincidat enim, si possibile est bk sectioni apud k. Et ordinate ducatur kt iam ipsi dbe tangenti, per additam 32^ae praemissi, equidistans²⁷.

Sitque ipsius be dupla bl.

// Igitur coniuncta az producatur: sitque azn ipsique bz²⁸ [A:40r]aequidistans tn.

//

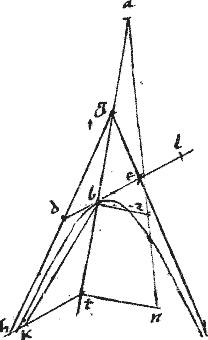
Quibus per actis, cum be possit quadrantem speciei sub ipsis ab bz contentae; iam bl²⁹ poterit ipsam speciem totam.

// Quare, per 16^am sexti Euclidis ipsae ab bl bz sunt continuae proportionales.

// Et ideo per 17^am 6ⁱ, sicut ab bz sic ab bl³⁰ et sicut³¹ gb be propter abl gbe similitudinem³². // Sed sicut ab bz sic at tn propter abz atn similitudinem. // Ergo sicut at tn sic gb be et sicut³³ gb bd (cum db be sint aequales) et sicut³⁴ bt tk (cum gbd btk sint similia).

// Verum, cum per 12^am primi Conicorum kt possit btn et ob id, bttktn sint continuae proportionales, atque ideo bt tk sit sicut bt tn, erit iam, sicut bt tn sic at tn.

// Quare, per 9^am 5ⁱ Euclidis ipsae bt ta sunt aequales: quod est absurdum.

// Igitur ipsi gd non tangenti parallelus acta per b summitatem sub signo b deducta semper intra sectionem cadit. Quod erat demonstrandum.