47a Si hyperbolen711, vel ellipsim, vel circuli periferiam linea tangens coincidat diametro: et per tactum et centrum linea ducatur, in ipsa sectione, per medium secabit ductas in sectione penes712 tangentem.
Sit hyperbole, vel ellipsis, vel circulus, beh. // Cuius diameter ab. // Centrum g. // Tangens de. // Punctum tactus e. // Et coniungatur ge. // Atque per utcumque relictum punctum n in periferia ducatur penes et713 tangentem linea nh // Quam ge producta secet apud o.
// Dico iam quod no aequalis est ipsi714 oh.
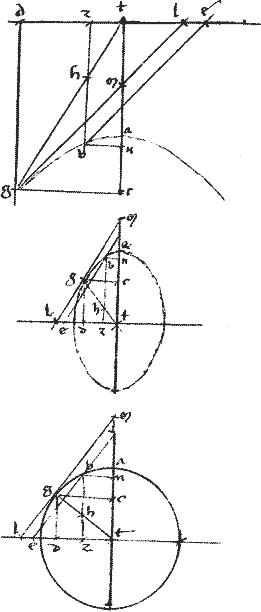
// Ducantur enim ordinate znx bl occurrentes ipsi ge apud puncta l x item hmc occurrentes715 ipsi geo productae apud m.
// Eritque per 43am huius, in hyperbola ![]() gcm aequale
gcm aequale ![]() gbl cum
gbl cum ![]() tch simul. //
tch simul. //
// Ablatoque communi ![]() gbl supererit
gbl supererit ![]() tch aequum
tch aequum ![]() bcml.
bcml.
// Rursumque per 43am ![]() gzx aequale erit
gzx aequale erit ![]() gbl cum
gbl cum ![]() tzn. // Ablatoque rursum communi
tzn. // Ablatoque rursum communi ![]() gbl supererit
gbl supererit ![]() tzn aequum
tzn aequum ![]() bzxl.
bzxl.
// In ellipsi autem, et circulo ![]() gcm cum
gcm cum ![]() tch erit per 43am aequale
tch erit per 43am aequale ![]() gbl.
gbl.
// Demptoque communi ![]() gcm: supererit
gcm: supererit ![]() tch aequale
tch aequale ![]() bcml.
bcml.
// Rursumque per 43am [A:29v] ![]() gzx cum
gzx cum ![]() tzn aequale est
tzn aequale est ![]() gbl.
gbl.
// Demptoque communi ![]() gzx supererit
gzx supererit ![]() tzn aequum
tzn aequum ![]() bzxl.
bzxl.
// Itaque tam in hyperbola716, quam in ellipsi, circuloque.
![]() tzn aequale est
tzn aequale est ![]() bzxl itemque
bzxl itemque ![]() tch aequum
tch aequum ![]() 717 bcml.
717 bcml.
// Qua[S:40]re et reliquum reliquo. Scilicet ![]() 718 nhcz aequale719 erit
718 nhcz aequale719 erit ![]() 720 mcxz721.
720 mcxz721.
// Commune auferatur pentagonum onzcm722. // Et supererit ![]() omh aequale
omh aequale ![]() oxm cumque talia
oxm cumque talia ![]()
![]() propter aequidistantiam basium sint similia; erunt et invicem aequilatera.
propter aequidistantiam basium sint similia; erunt et invicem aequilatera.
// Igitur ho on aequis angulis subtensae erunt invicem aequales. // Quod est propositum. Sed pro ipso n relicto puncto, capiatur ipsum b punctum. Hoc est, eat ho per summitatem sectionis. // Habebitque in tali casu linea bl vicem lineae znx.
// Et tunc per 43am in hyperbola ![]() gmc aequum est
gmc aequum est ![]() gbl cum
gbl cum ![]() bch.
bch.
// In ellipsi vero
et circulo

![]() gmc cum
gmc cum ![]() bch aequale
bch aequale ![]() gbl.
gbl.
// Quare, ablato utrinque ![]() gbl in hyperbola: et in ellipsi et circulo,
gbl in hyperbola: et in ellipsi et circulo, ![]() lo gmc723.
lo gmc723.
// Supererit utrobique724 ![]() bch aequale
bch aequale ![]() bcml.
bcml.
// Rursumque dempto ![]() bcmo communi.
bcmo communi.
// Supererunt ![]()
![]() omh olb aequalia725. // Quae quidem cum sint similia, propter aequidistantiam basium, erunt invicem aequilatera.
omh olb aequalia725. // Quae quidem cum sint similia, propter aequidistantiam basium, erunt invicem aequilatera.
// Quare ho ob aequos angulos respicientia latera invicem aequalia. // Quod est propositum. [A:30r] Ponatur [[etiam]]726 n contingenter relictum punctum ad reliquas sectionis partes.
// Et tunc per 43am in hyperbola ![]() gcm aequale erit
gcm aequale erit ![]() gbl cum
gbl cum ![]() tch.
tch.
// Ablatoque communi ![]() gbl supererit
gbl supererit ![]() tch aequale
tch aequale ![]() bcml. // Rursumque, dempto communi
bcml. // Rursumque, dempto communi ![]() tcmo supererit
tcmo supererit ![]() hom aequum
hom aequum ![]() btol.
btol.
// Item, quoniam, per 43am ![]() gzx aequum est
gzx aequum est ![]() gbl cum
gbl cum ![]() tzn et ablato communi
tzn et ablato communi ![]() gbl superest
gbl superest ![]() tzn aequale
tzn aequale ![]() bzxl.
bzxl.
// Apponatur commune ![]() tzxo. // Eritque
tzxo. // Eritque ![]() nox aequale
nox aequale ![]() btol.
btol.
// Fuit autem ![]() btol aequale
btol aequale ![]() hom.
hom.
Igitur ![]() hom aequum est
hom aequum est ![]() nox. Quae cum sint similia, erunt et invicem aequilatera.
nox. Quae cum sint similia, erunt et invicem aequilatera.
// Quare ho on respondentia latera invicem aequalia.
// Quod est propositum.
// In ellipsi autem et circulo, per 43am ![]() gmc
gmc ![]() tch simul aequalia
tch simul aequalia ![]() gbl. Item
gbl. Item ![]() tnz
tnz ![]() gzx simul aequalia
gzx simul aequalia ![]() gbl.
gbl.
|
// Demptoque communi ![]() gto supersunt
gto supersunt ![]()
![]() hom nox aequalia: quae cum sint727 similia, et ob id invicem aequilatera, erunt ho on respectiva latera invicem aequalia.
hom nox aequalia: quae cum sint727 similia, et ob id invicem aequilatera, erunt ho on respectiva latera invicem aequalia.
// Quod est demonstrandum.
[A:30v] //
Scholium
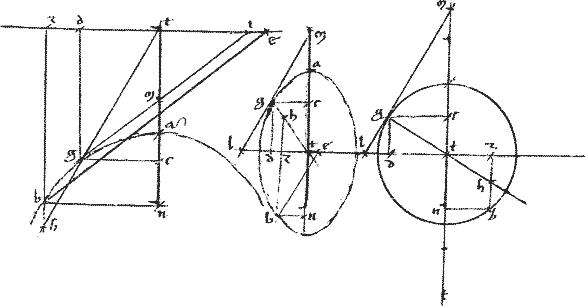
// Descriptio praesentis theorematis tam in hyperbola, quam in ellipsi et circulo tripliciter variatur, iuxta varium ipsius n, utcumque728 relicti puncti situm, atque ipsius hn ductum.
Non aliter ostendemus, quod, ipsa ge non solum ipsam hn sed omnes alias lineas intra sectionem penes de tangentem ductas singulas bifariam partitur. Et perinde, cum ab sit principalis diameter; ipsa ge erit ex generatione diameter. Et similiter demonstrabimus, quod omnis linea per sectionis centrum ducta in periferiam, erit ex generatione diametros in hyperbola729, ellipsi, circuloque.