[S:217]

PROPOSITIO XXIV

179 Spatium sub spira primae revolutionis et recta, quae revolutionis initium est, compraehensum est tertia pars circuli primi.

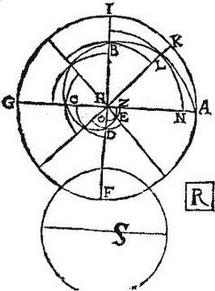
180 Sit spira primae revolutionis ABCDEH, cuius initium H et linea AH initium revolutionis, circulus primus AFGI, cuius tertia pars sit circulus S. 181 Ostendendum est, quod spatium sub linea spirali ABCDEH et sua AH recta compraehensum, aequale est circulo S. Secus enim erit aut maius, aut minus. 182 Sit, primum, minus dictum spatium spirale circulo S in spatio R, ita ut spirale spatium, una cum R sumptum, sit aequale circulo S. 183 Itaque, per 21^<am> huius eiusque corollarium, potest ipsi spirali spatio circumscribi figura ex similibus frustis composita, excedens ipsum spatium spirale minus quam sit R spatium. 184 Circumscribatur, sitque eius maximum frustum AHK, minimum vero EHZ: itaque maior erit circulus S, quam figura circumscripta. Et quoniam rectae a puncto H ad spiram eductae, per 10^<am> huius, sese continuatim excedentes excessu, qui aequalis est minimae, estque maxima AH et minima HE, et a singulis his fiunt similia frusta, sive similes formae, quae sunt similes circuli AFG sectores. 185 Propterea, per 8^<am> huius eiusque corollarium, totidem frusta, quot sunt dictae lineae, singula aequalia frusto maximo AHK, hoc est totus ipse circulus AFG minus erit quam triplum aggregati dictorum similium frustorum, quorum maximum AHK, minimum EHZ, hoc est ipsius figurae spiram circumscribentis; quippe quae constat ex huiusmodi similibus frustis. 186 Maior autem fuit circulus S, quam figura circumscripta. Eo magis circulus AFGI minor erit quam triplum ad circulum S; quod est contra hypothesim. Non est ergo spatium spirale minus circulo S.

187 Sed neque maius erit. Sit enim, si possibile est, spirale spatium sub spira ABCDEH et sub recta HA compraehensum maius circulo S in ipso spatio R, ita ut circulus S, una cum spatio R, sit iam aequale spatio spirali. 188 Deinde, per 21^<am> huius eiusque corollarium²⁰, ipso spatio spirali inscribatur figura ex similibus frustis composita, cuius maximum frustum sit NHL, minimum vero OEH, ita ut spirale spatium excedat figuram inscriptam minori spatio quam R. 189 Et quoniam rectae a puncto H ad spiram deductae, quarum maxima est HA, minima HE se continuatim excedunt excessu, qui aequalis est minimae per 10^<am> huius. Et a singulis fiunt similia frusta, quae sunt similes circulorum sectores, quorum maximus est AHK minimus vero OEH. 190 Propterea, per 8^<am> huius eiusque postremum corollarium, totidem frusta, quot sunt dictae lineae singula aequalia frusto maximo KHA, hoc est totus ipse circulus AFGI plusquam triplum, est aggregati dictorum similium frustorum (demp[S:218]to frusto AHK, quod ex maxima linearum, quae est AH conficitur) quae frusta componunt figuram inscriptam. 191 Maior autem est figura inscripta, quam circulus S. Quandoquidem circulus AFGI maiori excessu circulum S quam figuram dictam superavit. 192 Tanto magis ergo circulus AFGI plusquam triplus erit circuli S, quod rursum contra hypothesim est. 193 Non est ergo spatium spirale maius circulo S, sed neque minus fuit: superest ergo, ut aequale sit spatium spirale circulo S. Quod erat ostendendum.