PROPOSITIO XXIII

174 Sumpto spatio sub quacumque spirae peripheria et sub duabus rectis ab initio spirae ad peripheriam ipsius deductis, potest figura circumscribi et inscribi ex frustis similibus, ita ut circumscripta inscriptam excedat, minori spatio quam sit quodcumque datum spatium.

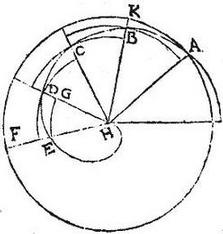
175 Sit quantacumque spirae portio ABCDE, quae cum rectis AH, HE a principio spirae H eductis spatium quodvis spiralem contineant. Oportet tali spatio figuram circumscribere et inscribere; ita ut proponitur. 176 Ad spatium HA super centro H describatur circulus AKF, cui HE producta occurrat apud F et angulus AHF per medium iterum atque iterum dividatur, donec deveniatur ad spatium, quod sit AHK dato spatio minus. Deinde, ut in praemissis, super H centro circulares peripheriae describantur per puncta spiralem lineam secantia. 177 Quibus ordine peractis, satisfactum esse proposito constabit. Nam figura, nunc exempli gratia spirali spatio circumscripta, constat ex quatuor frustis et ex totidem inscripta conflatur. Suntque frusta similia, similes videlicet circuli sectore. Cumque tria frusta inscriptae (minimo dempto) sint aequalia tribus frustis circumscriptae (maximo excepto) iam circumscripta tanto maior erit quam inscripta, quanto maximum frustum circumscriptae AHK excedit HEG minimum inscriptae, et perinde minori spatio quam sit datum spatium; quandoquidem totum AHK minus fuit dato spatio.

COROLLARIUM

178 Unde sequitur, ut circa tale spatium spirale describi possit et inscribi figura, ut dictum est, ita ut circumscripta super spiralem aream addat minus quovis dato spatio, et inscripta sit minor eadem area per excessum quovis dato spatio minorem.