F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de momentis aequalibus Liber quartus 8
<- App. -> <- = ->

PROPOSITIO VIII.

Si per centra partium, et centrum totius ducantur tria parallela plana: quod per centrum totius, medium erit planorum; portiones autem cuiuslibet rectae inter aequidistantia plana receptae sunt partialibus gravibus, ordine permutato, proportionales: unde si gravia sint aequalia portiones dictae erunt aequales, et e contrario.

Sint centra gravium partialium A, B, centrum commune amborum C, per quae ducantur tria plana, inter plana vero receptae portiones cuiuslibet rectae sint, DF, FE; demonstrandum est, quod planum, quod per punctum C ducitur cadit inter plana, quae [S:163] per puncta A, B: quodque linea EF ad FD est sicut grave A ad grave B: coniungantur enim A, B, eritque per 6. primi momentorum aequalium, C in ipsa AB linea; et proinde planum quod per C erit inter plana, quae per A, B puncta: item per 17. XI. Euclidis, sicut linea EF ad lineam FD, sic linea BC ad lineam CA, per 27. autem primi momentorum aequalium, sic grave A ad grave B.

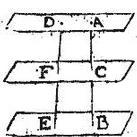
figura 12

Igitur sicut grave A ad grave B, sic linea EF ad lineam FD, quae fuerunt demonstranda.

Inizio della pagina
 ->