PROPOSITIO VII.
Solidi ex octo triangulis constructi, quorum bina opposita aequidistant, semper, et alterum alteri aequilatera sunt, hoc est octahedri corporis: centrum est in communi sectione trium axium.

Intelligatur planum parallelogrammum ABCD, cuius diametri AC, BD se vicissim per aequalia secantes in puncto G; ponaturque EGF perforans planum ut sint GE, GF aequales, et coniungantur puncta A, B, C, D, cum extremis E, F; sic enim fiet octahedrum solidum, quale proponitur ABCDEF, in quo binae quaelibet oppositae bases triangulae aequidistant, et aequilaterae sunt altera alteri, et in quo tres axes AC, BD, EF, se invicem bifariam secant in puncto G; demonstrandum est igitur quod centrum gravitatis octahedri ABCDEF est ipsum punctum G; construatur enim ipsi ABCDEF octahedro simile, et aequilaterum octahedrum HKLMNO, cuius axes HL, KM, NO se vicissim secent apud P punctum: deinde congruat parallelogrammum HKLM parallelogrammo ABCD: sic enim propter aequalitatem laterum, et angulorum congruent singula latera octahedri HKLMNO singulis lateribus octahedri ABCDEF, et singulae vertices singulis verticibus, et singuli axes singulis axibus, et octahedrum octahedro coaptabitur, ut ex duobus unum fiat: congruent itaque per sextum postulatum, octahedrorum centra. Rursum congruat parallelogrammum HKLM parallelogrammo ABCD commutatis angulis: sic enim congruent rursus axes axibus commutatis extremis: et rursum octahedrum octahedro coaptabitur: et rursum per dictum postulatum, solidorum centra congruent: quando igitur centra gravitatum congruunt in utraque coaptatione; nulla autem puncta solidorum in utraque coaptatione congruunt praeterquam puncta G, P quae sunt communes axium sectiones, propterea omnino ipsa G, P puncta erunt solidorum centra: quod erat demonstrandum. [S:162]
Alia demonstratio huius septimae.
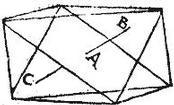
Sit octahedrum solidum A habens oppositas quasque bases parallelas: sitque A unum parallelogrammorum, quod basis est communis duarum quadrangularum pyramidum B, C componentium ipsum octahedrum; sitque parallelogrammi A, centrum punctum A: aio quod etiam A punctum erit centrum solidi octahedri A; quod sic ostendam. Sit pyramidis B centrum punctum B, et coniungatur BA, et producatur in rectum, ponaturque ipsi BA aequalis AC, eritque punctum C centrum pyramidis C per ultimum postulatum, quandoquidem pyramides A, B sunt similes, et aequales, et punctum A centrum basis earum communis, atque AB, AC lineas correlativas, et aequales habeant, sintque invicem aequales. Itaque puncta B, C sunt centra gravium aequalium pyramidum scilicet A, B: quare per 16. primi aequalium momentorum, aequaliter distant a centro totius; et per 6. eiusdem, centrum totius est in recta BC: sed punctum in recta BC, a quo puncta B, C aequaliter distant est punctum A. Igitur punctum A est centrum totius octahedri scilicet A: quod fuit ostendendum.
Similiter ostendam, quod centrum octahedri A est in centro cuiuslibet alterius parallelogrammi ex lateribus octahedri constituti.
Vel sic, cum per 4. secundi momentorum aequalium, centrum A parallelogrammi A sit in sectione bifariam diametrorum eiusdem parallelogrammi, atque eaedem diametri sint et diametri reliquorum duorum ex reliquis octahedri lateribus constitutorum parallelogrammorum: constat iam quod A punctum est centrum tam octahedri, quam uniuscuiusque parallelogrammi ex octahedri lateribus constituti.
COROLLARIUM
Hinc et illud infertur, quod octahedri talis centrum est semper in communi sectione axium solidi: nam axes sunt, qui coniungunt oppositos solidi angulos, et proinde ipsae parallelogrammorum diametri, in quarum sectione centrum octahedri fuisse demonstravimus.