PROPOSITIO XXIII.

Centrum gravitatis parabolici conoidis axem ita dividit, ut pars ad verticem reliquae ad basim sit dupla.

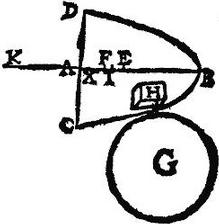
Esto conois parabolicus CBD, cuius axis AB, qui dividatur in E, ut AE tertia pars sit totius AB. Aio quod punctum E est centrum gravitatis solidi parabolici CBD. Si enim hoc verum non est; cadat centrum conoidis aut supra, aut infra punctum E in eodem axe AB, et primo cadat infra si possibile est in puncto X, et intelligatur figura inscripta conoidi ex cylindris aeque altis composita, cuius pars sexta altitudinis unius cylindrorum minor sit ipsa XE; ponatur esse EF: et quam proportionem habet AF ad FX, eamdem habeat solidum conoidale ad spatium G: deinde alia figura ex cylindris aeque altis eidem conoidali scribatur maior praecedente, quae componetur ex maiori multitudine cylindrorum minus altis, ideoque eorum sextantes minores erunt quam EF, quare maioris futurae inscriptae, centrum gravitatis cadet inter E, et F sit punctum I; defectus vero huius figurae inscriptae a conoidali minus sit spatio G, sit illud H: manifestum est rectam AI ad IX minorem proportionem habere, quam AF, ad FX, seu quam conoidale CBD ad spatium G, et ideo multo minorem rationem quam idem conoidale ad spatium H minus quam G; et disiunctim AX ad XI minorem proportionem habebit, quam figura postremo inscripta conoidi ad eius complementum H, seu ad defectum, quo minor est conoidali: augeatur ergo AX, itaut XK ad XI sit sicut figura inscripta conoidali ad eius residuum H ad conoidale spatium: quapropter in libra KI punctum X est centrum gravitatis totius conoidis CBD, punctum vero, I est centrum gravitatis unius partis, nempe figurae inscriptae ex cylindris aeque altis compositae; et sicut KX ad XI sic est figura inscripta ad spatium H seu ad defectum a conoide. Ergo per 27. primi momentorum aequalium punctum K erit centrum gravitatis praedicti defectus a conoide: unde centrum K cadet extra ambitum excessus conoidis supra figuram inscriptam, quod est absurdum per ultimum postulatum: non igitur fieri potest ut centrum gravitatis conoidis cadat infra punctum E versus A.

Ponatur secundo, si fieri potest centrum gravitatis conoidis supra punctum E ad partes B, ut in M: et facta consimili constructione, circumscribatur conoidi figura ex cylindris aeque altis composita, cuius centrum gravitatis sit N: et quam rationem habet AN ad NM, eamdem habeat solidum conoidale ad spatium G: postea circumscri[S:178]batur eidem conoidi alia figura.

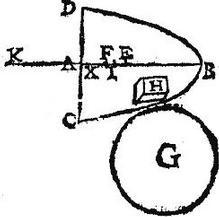
Ex cylindris aeque altis composita, minor praecedente, constans nimirum ex maiori multitudine cylindrorum; haec profecto habebit centrum gravitatis vicinius puncto E, quam praecedens maior figura circumscripta; cadet ergo eius centrum inter N, et E, sit illud O punctum: patet quoque excessum quo haec figura circumscripta conoidem superat minorem esse spatio G, sit illud H: hinc constat AO ad OM minorem proportionem habere, quam AN ad NM; seu quam conoidale CBD ad G, et adhuc minorem quam conois CBD ad spatium H; fiat ergo KO maior quam AO ad OM, sicut conoidale CBD ad spatium H, et quia in recta linea KM punctum O est centrum gravitatis totius figurae ex cylindris aeque altis compositae conoidi circumscriptae: et punctum M est centrum gravitatis unius partis eiusdem figurae circumscriptae, scilicet conoidis CBD; et sicut KO ad OM, sic se habet idem conoidale ad spatium H, scilicet ad excessum figurae circumscriptae supra conoidem, ergo per 27. primi aequalium momentorum punctum K erit centrum gravitatis praedicti excessus figurae circumscriptae supra conoidem, hoc autem cadit extra ambitum praedicti. Excessus; quod est impossibile, et contra 8. postulatum non ergo possibile est ut centrum conoidalis cadat supra punctum E ad partes B; sed neque infra punctum E reperiri posse ostensum est, sequitur ergo ut centrum gravitatis conoidis praecise existat in puncto E axim dividente ut BE dupla sit ipsius EA quod propositum fuerat.