PROPOSITIO XXII.
Si conoidi parabolico ascribantur duae figurae ex cylindris scalatim aeque altis compositae: centrum gravitatis figurae inscriptae in axe distabit basi conoidis minus triente, figurae vero circumscriptae centrum gravitatis distabit maius triente totius axis; eritque defectus, vel excessus aequalis sextanti altitudinis cuiuslibet cylindrorum.
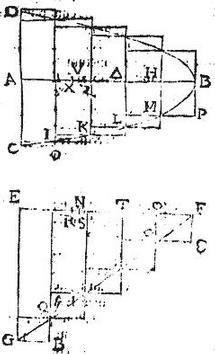
Esto conois parabolicus CBD, cuius axis AB, basis vero circulus radio AC descriptus; huic vero solido ascribantur duae figurae ex cylindris aeque altis compositae inscripta AIKMH; circumscripta vera AOPB; seceturque AV pars tertia axis AB, et hinc inde abscindantur portiones VX, VZ singulae aequales sextanti ipsius HB altitudinis nempe unius cylindrorum. Aio quod punctum X est centrum gravitatis figurae inscriptae; Z vero est centrum gravitatis figurae circumscriptae. Exponatur triangulum EFG rectangulum in E cuius latus EF aequale sit axi conoidis AB; seceturque EF in totidem partes aequales, ac dissectus fuerat axis AB; ascribanturque triangulo duae figurae ex parallelogrammis scalatim dispositis, et aeque altis, et tot numero, quot sunt cylindri in conoidali; sitque inscripta figura EQYOα, circumscripta vero EBε F; seceturque ex libra EF portio EN tertia pars totius, et NR, atque NS aequales sextanti altitudinis cuiuslibet parallelogrammi. Postea quia in conoidali bases abscissae, quae bases quoque sunt cylindrorum aequalium altitudinum LH, MB, etc. circuli sunt nempe descripti radiis Δ L, et HM, hi vero circuli eamdem rationem habent quam quadrata radiorum per 2. tertii decimi elementorum Euclidis et in parabola sicut quadratum Δ L ad quadratum HM sic est per 20. primi conicorum Apollonii portio axis Δ B ad HB, estque TF ad α F in eadem ratione, cum sint aequales hae illis, scilicet sicut TY ad α O, nempe ut parallelogrammum Yα ad parallelogrammum α ε cum sint eiusdem altitudinis. Igitur cylindrus HL ad cylindrum HP eamdem rationem habebit, quam parallelogrammum α Y ad parallelogrammum α ε: idem ostendetur de reliquis omnibus cylindris, et parallelogrammis figurarum inscriptarum, et circumscriptarum correlativa semper comparando. Cum igitur sint duae librae aequales AB, et EF in partes aequales dissectae in quibus suspenduntur ex aequalibus distantiis pondera proportionalia nempe cylindri in conoidali, et parallelogramma in triangulo similiter disposita, nempe consequenter a terminis B et F crescendo iuxta seriem numerorum ab unitate igitur per propositionem 21. praecedentem, centra [S:177] gravitatum correlativarum figurarum abscindent ex libris portiones aequales, similiter dispositas; sed per 20. centrum gravitatis figurae inscriptae in triangulo suspenditur ex puncto R. Igitur figurae inscriptae in conoidali centrum erit X punctum; quandoquidem ambo puncta X, R aequaliter recedunt a basibus, cum AV, et EN sint tertiae partes aequalium librarum AB, et EF, atque VX, et NR sint sextantes aequalium altitudinum HB, et α F. Eodem ratiocinio ostendentur puncta Z et S suspensionum loca esse centrorum figurarum circumscriptarum, quapropter propositio verificatur.