F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de momentis aequalibus Liber quartus 18
<- App. -> <- = ->

PROPOSITIO XVIII.

Si in quolibet cono ducatur planum basi aequidistans, et ita secans conicum axem, ut portio ad basim recepta sit tertia pars reliquae: centrum facti circuli erit centrum coni.

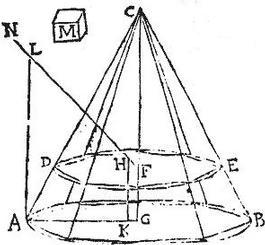
figura 26

Sit conus ABC, cuius basis AB circulus; vertex C punctum, secetque conum aequidistans AB circulo planum faciens circulum DE, secansque conicum latus AC in puncto D: itaut AD sit pars tertia ipsius DE: sitque centrum circuli DE punctum F. Aio quod F centrum est, et coni ABC. Coniungatur enim CF, et producatur, erit enim axis coni, cadetque in centrum basis AB, quod sit G: itaque si F non est centrum coni ABC; sit, si possibile est, aliud quam F punctum, quod sit H, ubicumque cadat, et coniungatur FH, et producatur, donec ipsi AL, quae axi conico CG aequidistat apud L punctum coincidat, et ulterius: item coniungatur AG, cui apud K coincidat ipsa HK aequidistas ipsi CG; quibus peractis, sicut est linea AK ad lineam KG, hoc est sicut linea LH ad lineam HF; sic stet pyramis quaedam laterata ABC intra conum descripta ad solidum M; et rursus sectis arcubus circuli AB singulis bifariam, iterum, atque iterum, inscribatur intra conum pyramis laterata, donec relictae portiones inter superficiem pyramidis, et coni sint minus solido M: quo facto pyramis talis, quae sit ABC habebit rationem maiorem ad relictas portiones, quam linea AK ad lineam KG, hoc est quam LH ad HF: sit ergo sicut pyramis ipsa ABC ad [S:172] relictas portiones, sic linea NH ad lineam HF; cumque centrum totius coni sit H, centrum autem unius partium; scilicet pyramidis ABC: sit F per praecedentem, (quandoquidem F centrum circuli DE est per corollarium secundae secundi aequalium momentorum, centrum rectilinei DE) necesse erit ut centrum reliquae partis, scilicet relictarum portionum sit N punctum: secus enim non essent gravia reciproca distantiis, quibus eorum centra absunt a centro communi: quod esset absurdum per 27. primi momentorum aequalium.

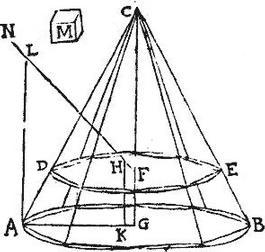
figura 27

Et si N centrum est relictarum portionum, sic centrum gravitatis est extra ambitum gravis. Quod per ultimum postulatum, est inconveniens: similiter demonstrabimus, quod centrum coni ABC nullum aliud esse potest, quam ipsum F punctum: erit ergo ipsum F punctum; sicut proponitur demonstrandum.

COROLLARIUM.

Manifestum est igitur, quod centrum gravitatis coni est in illo puncto unici axis, quod sic secat ipsum, ut portio ad basim recepta sit tertia pars reliquae.

Inizio della pagina
 ->