PROPOSITIO XVII.

Si in qualibet pyramide ducatur planum basi aequidistans, et ita secans unamquamque hypothemisarum, ut portio ad basim recepta sit tertia pars reliquae: centrum facti rectilinei erit centrum pyramidis.

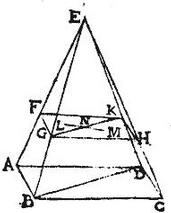
Esto exempli gratia pyramis ABCDE super quadrilateram basim ABCD, et sub vertice E, atque ducatur planum aequidistans basi ABCD, et secans unamquamque hypothemissarum, ut pote ipsam AE in puncto F; itaut portio EF sit tripla ipsius FA, et faciens in pyramide quadrilaterum FGHK iampridem simile ipsi quadrilatero ABCD. Demonstrandum est, quod centrum facti quadrilateri FGHK est et centrum pyramidis ABCDE: coniungantur enim BD, GK, et intelligatur pyramis tota divisa in duas pyramides triangulares, quarum bases triangulae ABD, BCD: eritque per 12. huius, centrum pyramidis ABDE centrum ipsum trianguli FGK, sit illud L punctum. Itemque centrum pyramidis BCDE centrum ipsum trianguli GHK, sit ipsum M punctum; et coniuncta LM erit per 6. primi aequalium momentorum centrum quadrilateri FGHK in linea LM: sit illud N: eritque per 27. praedicti, sicut triangulum FGK, ad triangulum GHK, sic linea MN ad lineam NL; sicut autem triangulum FGK ad triangulum GHK, sic triangulum ABD ad triangulum BCD: et perinde sic pyramis ABDE ad pyramidem BCDE: igitur sicut pyramis ABDE ad pyramidem BCDE, sic linea MN ad lineam NL. Quare per 28. memorati; quando partialium pyramidum centra sunt M, L: erit totalis pyramidis ABCDE centrum N punctum, quod fuit quadrilateri FGHK centrum. Quod fuit demonstrandum. Similiter idipsum ostendemus de pyramide pentagona, hexagona, et quodlibet deinceps laterum basim habente. Quemadmodum proponitur demonstrandum. [S:171]

COROLLARIUM.

Quando igitur per 13. huius, centra pyramidum triangularium sunt in lineis, quae centra basium trigonarum cum vertice coniungunt, atque in ipso rectilineo FGHK per 12. iam necesse est, et centrum totalis pyramidis ABCDE esse in linea, quae centrum totalis rectilinei ABCD cum ipso vertice coniungit, atque in centro facti rectilinei FGHK, hoc est in ipso puncto coniunctae lineae, quae portionem ab basim suscipit tertiam partem existentem residuae. Et e contrario necesse est, ut linea quae verticem pyramidis cuiuslibet cum centro pyramidis coniungit, producta cadat in centrum basis, hoc est ut linea EN producta cadat in centrum ABCD rectilinei. Namque bases triangulae, et omnes bases partiales tam in rectilineo ABCD, quam in rectilineo FGHK sunt ad invicem, sicut pyramides, quarum sunt bases, et perinde centra basium in facto rectilineo FGHK semper sunt eadem cum centris pyramidum, quarum sunt bases, et lineae a vertice E per talia centra ductae cadunt in centra basium dictis pyramidibus respondentium in ipso rectilineo ABCD, propter similitudinem triangulorum superiorum cum inferioribus, et proportione linearum; unde, et linea a vertice per centrum totalis pyramidis cadet in centrum totalis basis.