PROPOSITIO V.
Contra si per centrum gravitatis ipsius trapetii ducatur linea parallelus lateribus parallelis; ducta ita secabit unumquodque reliquorum laterum, ut segmentum aequidistantium laterum maiori conterminum ad reliquum eam habeat rationem, quam aggregatum ex duplo minoris aequidistantium laterum, et ex minori ad aggregatum ex duplo maioris, et ex minori.
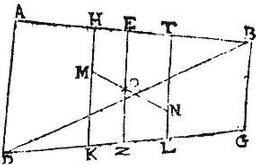
Hoc est si per centrum gravitatis trapetii ABG, quod sit O punctum ducatur EZ ipsis AD, BG parallelis lateribus aequidistans. Dico quod AE ad EB erit sicut aggregatum ex duplo ipsius BG minoris, et ex AD maiori aequidistantium ad aggregatum ex duplo ipsius AD maioris, et ex BG minori: quod sic ostendetur: per centra M, N triangulorum ABD, DBG ducantur HK, TL ipsis AD, BG paralleli: eruntque per 6. primi momentorum aequalium, centra M, O, N in una recta: et quoniam per 27. praedicti, gravia reciproca sunt distantiis, quibus eorum centra removentur a communi centro, ideo erit sicut linea MO ad ON, sic triangulum BDG ad triangulum ADB: sed per primam sex Euclidis, triangulum BDG ad triangulum ADB; est iam sicut basis BG ad basim AD, igitur, et sicut BG ad AD, sic MO ad ON: verum per 2. sex Euclidis.
Sicut MO ad ON, sic HE ad ET. Igitur
sicut HE ad ET. sic BG ad AD. Et coniunctim
|
|
quandoquidem HK, TL paralleli eunt per centra triangulorum ABD, BDG:
| ergo apposita utrobique ET erit BE aequalis |
|
| sicut BE ad ET. sic |
| ad AD. Et similiter ostendemus quod |
| sicut AE ad EH. sic |
| ad BG. Et permutatim erit. |
|
|
COROLLARIUM I.
Ex his iam manifestum est, quod si in trapetio, cuius duo tantum latera aequidistant, alterum ex reliquis lateribus in tria aequalia dividatur, et media tertia rursum in puncto quodam secetur, ut segmenta reciproca sint lateribus aequidistantibus; linea iisdem lateribus aequidistans ducta per punctum illud ibit per centrum gravitatis trapetii; hoc enim ostensum est in quarta praemissa.
COROLLARIUM II.
Contra si per centrum gravitatis trapetii ducatur linea lateribus parallelis, aequidistans: ducta sic secabit mediam tertiam utriuslibet reliquorum laterum trifariam divisi, ut segmenta reciproca sint lateribus aequidistantibus; hoc est ordine permutato proportionalia: et hoc in praecedenti 5. fuit demonstratum.
Alia demonstratio eiusdem quintae.
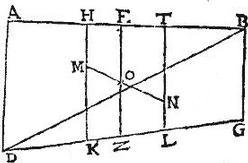
Esto trapezium ABGD cuius latera AD, BG aequidistent: ductaque diametro BD, divisaque per medium in puncto X: in productis AX, XG puncta sumantur M, N; ita ut tam AM ipsius MX, quam et GN ipsius NX dupla sit: eruntque per 25. secundi momentorum aequalium puncta M, N centra triangulorum ABD, DBG. Itaque coniuncta MN recta ponatur MO, ad ON sicut BG ad AD, hoc est sicut triangulum DBG ad triangulum ABD; eritque per 28. primi momentorum aequalium punctum O centrum aggregati ex triangulis dictis, hoc est centrum totius trapezii ABGD: ducatur ergo ipsis AD, BG parallelus OE occurrens lateri AB in puncto E. Et demonstrandum erit quod AE ad EB erit sicut duplum ipsius BG una cum AD ad duplum ipsius AD una cum BG. Hoc modo, ducantur ipsi OE paralleli ad dictum usque latus MH, NT, XP: eritque AP ipsi PB aequalis quoniam DX ipsi XB aequalis fuit; et similiter tam AH ipsius HP, quam BT ipsius TP dupla: secentur per [S:138] medium HA, BT singulae in punctis R, S; eruntque sex portiones AR, RH, HP, PT, TS, SB inter se aequales: erit autem sicut MO ad ON, hoc est sicut BG ad AD, sic HE ad ET, propter aequidistantiam linearum; ponatur HK aequalis ipsi HE, itemque TL aequalis ipsi TE: eritque per conceptionem AK aequalis ipsi ET; itemque BL aequalis ipsi EH: quamobrem linea AE constabit ex duplo ipsius EH (quod est KE) et ex ipsa ET (quae est AK): item linea EB constabit ex duplo ipsius ET (quod est EL) et ex ipsa EH (quae est BL); sed quoniam fuit sicut BG ad AD, sic HE ad ET: idcirco propter proportionalitatem talem bis arguendo per coniunctam proportionem erit sicut duplum ipsius BG cum AD ad duplum ipsius AD cum BG, sic iam linea AE ad lineam EB; quod fuit demonstrandum.
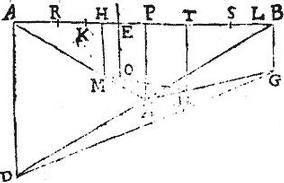
Huius autem propositionis conversa, quae est quarta huius demonstrabitur ex hac indirecte sicut in secunda parte sextae sequentis perficietur.