PROPOSITIO X.
Quod proposuit octava praecedens aliter demonstrare.
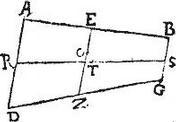
Esto trapetium ABGD, cuius axis RS per aequalia secans aequidistantia latera AD, BG in punctis R, S; in quo centrum gravitatis trapetii sit punctum O, in axe enim est centrum per 2. huius; quod centrum potest, et sic determinari: coniungantur RB, BD, DS, et divisa AB in tres partes aequales in punctis H, T, ducantur ipsis AD, BG aequidistantes HK, TL, quarum HK coincidat ipsis BR, RS, DG apud M, P, K puncta: ipsa vero TL coincidat ipsis RS, SD, DG apud Q, N, L puncta: eritque per 28. praecedentis, centrum trianguli ABD, punctum M: centrum vero trianguli BGD punctum N. Quare per 6. primi aequalium momentorum, centrum commune triangulorum ABD, BGD, hoc est centrum trapetii totius ABGD erit in linea MN: sed per 2. huius, centrum ipsius trapetii ABGD est in linea RS: igitur erit in communi sectione linearum RS, MN, quod sit O punctum:
|
|
| Atque |
| simul aequalia sunt ipsi OS. quandoquidem aequales sunt portiones RP, PQ, QS. |
|
SCHOLIUM
Et haec est demonstratio Archimedis praeclarissimi, ex qua indirecte potest demonstrari eius conversa, quemadmodum in prima demonstratione praecedentis nonae factum est; et quoniam demonstratio huius decimae non indiget, quemadmodum octava, quinque propositionibus praecedentibus octavam ipsam: idcirco ex hac decima rursum alio modo possent demonstrari propositiones praedictae.