F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de momentis aequalibus Liber secundus 6
<- App. -> <- = ->

PROPOSITIO VI.

Si per centra similium triangulorum aequidistantes correlativis lateribus agantur, actae ad eandem rationem secabunt reliqua latera.

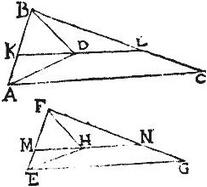
figura 8

Sunto duo triangula similia ABC, cuius centrum D, et EFG, cuius centrum H, et per centra D, H ducantur ipsis AC, EG basibus correlativis aequidistantes KDL. MHN secantes apud K, L, M, N triangulorum latera. Aio quod sicut AK, ad KB sic EM ad MF: coniungantur enim AD, DB, EH, HF, eruntque per 7. postulatum, triangula ADB, EHF similia; quandoquidem similium triangulorum ABC, EFG, centra sunt D, H: igitur anguli BAD, FEH aequales: sed anguli BAC, FEG per hypothesim aequales: ergo anguli DAC, HEG residui aequales. Quare, et eorum coalterni ADK, EHM aequales; unde in triangulis ADK, EHM reliqui anguli AKD, EMH sunt aequales: similia igitur sunt triangula ADK, EHM quando aequiangula sunt: et perinde residua triangula KDB, MHF aequiangula, et perinde similia inter se sunt. Quamobrem per 4. sex Euclidis, eorum latera proportionalia: hoc est in triangulis ADK, EHM, sicut iam est AK, ad EM, sic KD ad MH: in triangulis autem KDB, MHF, sicut est KD ad MH, sic KB ad MF: igitur sicut KB ad MF sic AK ad EM: et permutatim: sicut AK ad KB, sic EM ad MF: quod fuit demonstrandum: et per 2. sex Euclidis, ad eandem rationem secantur latera reliqua BC, FG, in ipsis L, N punctis: quemadmodum proponitur.

Inizio della pagina
 ->