PROPOSITIO III.
Centrum gravitatis in parallelogrammo est punctum, in quo diameter per aequalia secatur.

Sit parallelogrammum ABCD, in quo diameter AC secetur per medium in puncto E: aio quod E centrum gravitatis est parallelogrammi ABCD: namque parallelogrammum ABC per diffinitionem, grave uniforme est: agatur igitur per punctum E linea ipsis BC, AD lineis aequidistans FEG, quae per 2. sex Euclidis secabit per aequalia tam latus AB, quam latus CD: Unde triangula AEF, CEG invicem aequilatera erunt, et ideo linea FE aequalis lineae EG: cumque FG sit axis ipsius gravis uniformis ABC: erit per 25. praecedentis libelli, E centrum ipsius gravis ABC: quod fuit demonstrandum.
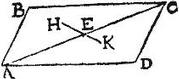
Sed et aliter idem demonstratur sic: sit per 5. praecedentis, inventum in triangulo ABC centrum gravitatis H, et in triangulo CDA centrum gravitatis K, et coniungantur HE, EK: iam triangulum CDA superpositum triangulo ABC congruet, (quandoquidem inter se aequilatera sunt:) quare per 6. postulatum, congruet centrum K centro H, et linea EK lineae EH: aequales ergo erunt anguli CEK, AEH ut qui coaptati congruant: sed per 13. primi Euclidis, anguli CEK, KEA simul aequales sunt duobus rectis: igitur, et anguli [S:114] AEH, KEA simul aequales sunt duobus rectis:

quare per 14. primi Euclidis, lineae HE, EK sunt una recta linea (et inter se aequales, quoniam congruunt: sunt autem triangula ABC, CDA inter se aequalia: et ideo per 16. praecedentis, aequaliter distant eorum centra H, K a communi centro, quod per 6. eiusdem, est in linea HK: punctum autem in linea HK, a quo centra H, K aequaliter distant, est punctum E: igitur punctum E est commune centrum ipsorum triangulorum ABC, CDA, hoc est parallelogrammi ABCD: quod erat demonstrandum.