PROPOSITIO II.

Centrum gravitatis rectilinei aequilateri, et aequianguli est idem, quod et magnitudinis.

Sit triangulum aequilaterum, et ideo aequiangulum ABC, cuius gravitatis centrum sit D. Aio quod D est centrum magnitudinis trianguli ABC, hoc est centrum circuli circumscribentis triangulum: exponatur enim ipsi ABC triangulo equilaterum triangulum EFG in quo centrum gravitatis sit H, et coniugantur centra gravitatum [S:113] D, H cum angulis, et coaptetur triangulum EFG triangulo ABC, ut punctum E puncto A, punctum F puncto B, et punctum G puncto C congruat, sic enim linea EH congruet lineae AD, et linea FH lineae BD, et linea GH lineae DC, quandoquidem per sextum postulatum centrum gravitatis H congruet centro gravitatis D, congruentibus iam figuris.

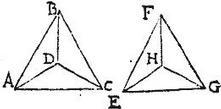
Rursum commutatis angulis coaptetur triangulum EFG triangulo ABC, ita scilicet, ut angulus F angulo A, angulus G angulo B, et angulus E angulo C congruat: sic enim rursum congruet per dictum postulatum, centrum gravitatis H centro gravitatis D; et ideo linea FH congruet lineae AD, linea GH lineae BD, linea EH lineae CD: quamobrem linea FH, quae in prima triangulorum coaptatione congruebat lineae BD: nunc in secunda, congruet lineae AD: igitur lineae AD, BD sunt aequales quandoquidem ab eadem linea FH mensurantur. Item linea GH, quae prius congruebat lineae DC, nunc congruit lineae BD, et ob id lineae BD, DC aequales, quandoquidem eidem GH congruunt: ergo omnes tres lineae AD, BD, DC sunt aequales: quapropter punctum D centrum magnitudinis est in triangulo ABC, quandoquidem aeque removetur ab extremis: similiter idipsum demonstrabimus in quacumque figura aequilatera, et aequiangula: quod quidem proponebatur demonstrandum.

COROLLARIUM.

Unde simul manifestum est, quod in omni figura aequilatera, et aequiangula centrum gravitatis, et centrum circuli circumscribentis figuram ipsam est.