F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de momentis aequalibus Liber secundus 28
<- App. -> <- = ->

PROPOSITIO XXVIII.

Si linea a quolibet angulo trianguli producta subtensum latus per medium secet, et alia eidem lateri aequidistans suscipiat reliquorum laterum portiones ad dictum angulum duplas relictarum; punctum in quo productae se invicem secant est centrum gravitatis trianguli.

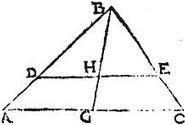
figura 32

In triangulo ABC ab angulo quolibet, ut B, producta linea BG basim AC per aequalia secet in puncto G, linea vero ipsi AC aequidistans DE abscindat portiones BD, BE duplas ipsarum DA, EC secans ipsam BG apud H: demonstrandum est, quod punctum H centrum est trianguli ABC; sic, nam cum DH aequidistet ipsi AG, atque BD dupla sit ipsius DA: iam per 2. sex Euclidis, et BH dupla erit ipsius HG: quare per 25. huius, H centrum erit trianguli ABC.

Vel procede sic: nam cum BG secet per aequa latus AC oppositum: iam per 23. huius, it per centrum trianguli ABC: item cum DE aequidistans lateri AC suscipiat portionem BD duplam ipsius DA: iam per 15. huius, ibit et per centrum trianguli ABC: omnino igitur trianguli ABC centrum erit communis huiusmodi linearum sectio, quod est ipsum H punctum; quod erat demonstrandum: et haec de centro gravitatis trianguli satis.

Inizio della pagina
 ->