F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de momentis aequalibus Liber secundus 27
<- App. -> <- = ->

PROPOSITIO XXVII.

Quod decima octava huius proposuit aliter demonstrare.

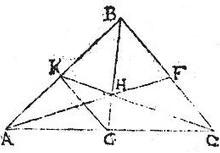
figura 31

In triangulo ABC ducatur uni laterum ut pote AC aequidistans linea DE, et reliqua latera apud puncta D, E ita secans, ut BD, BE portiones duplae sint reliquarum DA, EC; et ipsa DE per aequalia secetur in puncto H: demonstrandum est quod H punctum est gravitatis centrum trianguli ABC; per alia media, quam in 18. huius, ostensum est. Sic, coniungatur BH, quae producta coincidat basi AC in puncto G. Itaque quoniam aequidistat DE ipsi AC, et per aequalia secatur apud H, idcirco ex similitudine triangulorum, et AC per medium secatur apud G: quare per 23. huius, linea BG per centrum trianguli ABC incedit; est et BH dupla ipsius HG per 2. sex Euclidis, [S:129] quando aequidistat DH ipsi AG: etBD dupla est ipsius DA. Igitur per 25. praecedentem, H punctum est centrum gravitatis trianguli ABC: quod demonstrandum fuit: quae demonstratio quoniam innititur 23. quae non indiget adminiculo duodecim propositionum immediate praecedentium, stat sine earumdem auxilio: et idcirco dictae duodecim propositiones rursus ex hac 27. novo medio demonstrari possent; quod nos exercitio perspicacis ingenii relinquimus.

Inizio della pagina
 ->