F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de momentis aequalibus Liber secundus 21
<- App. -> <- = ->

PROPOSITIO XXI.

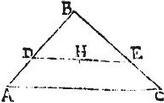
figura 24

Si ab angulo cuiuslibet trianguli per centrum gravitatis linea ducatur, producta per aequalia secabit subtensum latus.

In triangulo ABC ducatur a quovis angulo, ut pote B, per centrum trianguli, quod sit H linea BH, quae producta coincidat opposito lateri AC apud G punctum: aio quod AC latus [S:125] per aequalia secatur apud G punctum: ducatur enim per centrum H ipsi AC aequidistans linea DHE: eruntque per praecedentem ipsae DH, HE portiones aequales: sed propter aequidistantiam linearum DE, AC, et similitudinem triangulorum ABG, DBH; et similitudinem triangulorum BHE, BGC, erit sicut AG ad DH, sic BG ad BH: et sicut BG ad BH, sic GC ad HE: igitur, et sicut GC ad HE, sic AG ad DH: et permutatim, sicut AG, ad GC, sic DH ad HE; fuit autem DH aequalis ipsi HE. Ergo, et aequalis erit AG ipsi GC: itaque AC per aequalia secatur apud ipsum G punctum: quod erat demonstrandum.

Inizio della pagina
 ->