PROPOSITIO XXXVII.

Gravia ab aequis spatiis pendentia sunt momentis proportionalia.

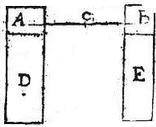
Duo gravia A, B pendeant ab aequalibus spatiis AC, CB: aio quod sicut grave A ad B, sic est momentum A ad momentum B: quod sic demonstrabitur. Sit ipsius gravis A multiplex ad libitum grave AD; itemque ipsius gravis B multiplex secundum quemvis numerum grave BE: sic enim per praecedentem, quam multiplex est grave AD gravis A, tam multiplex erit, et momentum AD momenti A; et per eandem, quam multiplex est grave BE gravis B, tam multiplex erit, et momentum BE momenti B: habemus igitur quatuor magnitudines: primam grave A, secundum grave B, tertiam momentum A, quartam momentum B: primae autem, et tertiae assignatae sunt aeque multiplices, grave AD, et momentum AD: secundae item, et quartae sunt, et aeque multiplices, grave BE, et momentum BE: et quoniam aequalia supponuntur spatia AC, CB: ideo per 18. huius, si grave AD aequale est gravi BE, iam ipsi aequeponderat, hoc est per diffinitionem aequale est momentum AD momento BE: si autem grave AD maius est gravi BE: iam per 21. huius, et grave AD deorsum feretur, hoc est per diffinitionem maius est momentum AD momento BE: et per eandem, si minus est grave AD gravi BE, feretur deorsum ipsum BE, hoc est minus erit momentum AD momento BE: itaque si multiplex primae maior est multiplice secundae, et multiplex tertiae maior erit multiplice quartae: et si minor, minor; et si aequalis, aequalis: atque idipsum evenit quibuscumque multiplicibus eodem ordine sumptis. Quamobrem per diffinitionem proportionalium magnitudinum in quinto elementorum positam, memoratae quatuor magnitudines proportionales erunt: hoc est prima ad secundam, sicut tertia ad quartam: grave scilicet A ad grave B, sicut momentum A ad momentum B: quod fuerat demonstrandum.