PROPOSITIO V.

Iisdem suppositis, si per lineam, quae tangit sectionem factam a plano per axem ducatur planum rectum plano per axem: ductum planum tanget solidum in eo puncto, in quo praedicta linea tangit sectionem.

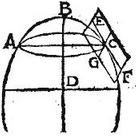
In eadem enim descriptione, facta sectio a plano per axem solidi ducto, est ipsa ABC, linea tangens eam sectionem est ECF, quandoquidem in plano tangenti apud C, constituta extra solidi superficiem, et perinde extra sectionem ABC cadit; punctum quoque contactus C. Dico itaque, quod planum ductum per ECF rectum super plano ABC tangit solidum in ipso C puncto; secus enim sit aliud planum tangens solidum apud C punctum: itaque planum ABC per axem per tertiam praecedentem rectum erit plano tangenti; sed et idem per hypothesim, rectum est plano per ECF. Igitur per decimam nonam 11. communis sectio plani tangentis, et plani per ECF perpendicularis erit super planum ABC: erit ergo talis communis sectio linea GC, quippe quae per C commune punctum planis incedit, et super ABC planum perpendicularis est. Igitur tangens planum ducitur per GC lineam; et perinde secat ipsum ABC planum, et communis sectio ibit per C punctum: quare per 32. primi conicorum cadet intra sectionem ABC, cum linea ECF tangat sectionem; et ideo planum, quod tangere supponebatur, secabit sectionem; quod est absurdum; nullum igitur planum ductum per ECF lineam nisi rectum plano ABC tangit in ipso C puncto solidum. Quod fuit demonstrandum.