PROPOSITIO X.

Omnis portio parabolici solidi, plano super axem recto abscissa Sexquialtera probatur esse coni basim, et axem eumdem cum portione habentis.

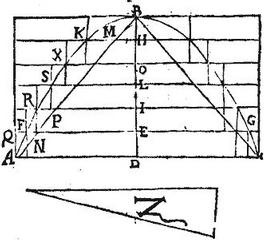
Esto portio conoidis parabolici ABC, cuius axis BD, quod sectum plano per axem faciat parabolem ABC per 17. praemissi; cuius plani cum plano portionem abscindente communis sectio sit recta AC: erit per 17. praemissi, sectio in solido facta per planum abscindens, circulus cuius diameter AC, super quem circulum conus constituatur habens verticem B, axemque BD. Demonstrandum est itaque, quod portio conoidis solidi parabolici ABC sesquialtera est coni ABC: exponatur conus Z sesquialter coni ABC. Item cylindrus basim habens circulum AC, axem autem BD; qui cylindrus cum sit per 15. praemissi, triplus coni ABC; iam ad conum Z duplus erit. Dico ergo, quod portio conoidis ABC aequalis erit cono Z; secus enim erit aut maior, aut minor: sit primum maior portio conoidis ABC cono Z aliquo excessu. Itaque per 8. huius, et per corollarium praemissae potest inscribi portioni ABC figura quaedam ex cylindris composita; itaut portio ABC addat super figuram inscriptam minus dicto excessu; et perinde inscripta figura sit maior cono Z. Inscribatur, sitque maximus cylindrorum componentium talem figuram inscriptam cylindris FGD, cuius basis diameter FEG, axisque ED, minimus autem cylindrus KOH, cuius basis, semidiameter KH axisque HO: item sit ABC triangulum per axem in cono ABC. Et producantur plana distinguentia cylindros figurae inscriptae, donec secent cylindrum magnum ABC in cylindros aequales. partes autem axis BD receptae a vertice B ad singulas cylindrorum bases vocentur katheti, quorum maximus BD, minimus vero BH, lineae autem aequidistantes inter axem BD, rectamque AB vocentur bases, quarum maxima AD, minima vero HM: item lineae receptae ab axi BD ad peripheriam parabolae AKB vocentur ordinatae, quarum maxima AD, [S:254] minima vero HK. Demum lineae receptae ab axi BD ad latus usque cylindri ABC, quae sunt aequales ipsi AD vocentur paralleli: quibus acceptis sit argue. Quoniam cylindri eiusdem altitudinis sunt sicut bases, et bases sicut quadrata semidiametrorum: ideo sex cylindri aequales, in quos secatur cylindrus ABC ad quinque cylindros figurae conoidi parabolico inscriptae, sunt sicut sex quadrata AD ad quinque quadrata reliquarum ordinatarum EF, RI, HK, et cetera quippe quae sunt semidiametri basium quinque cylindrorum. Sex autem quadrata AD ad quinque quadrata reliquarum ordinatarum sunt per 20. primi conicorum elementorum sicut sexcuplum axis BD, seu katheti ad aggregatum reliquorum kathetorum EB, IB, HB, et cetera et propter similitudinem triangulorum sicut sexcuplum basis AD ad aggregatum reliquarum basium EN, IP, HM, et cetera igitur sicut sexcuplum basis AD ad aggregatum reliquarum basium EN, IP, HM, et cetera sic sex cylindri in principio ducti, hoc est totus cylindrus ABC ad quinque cylindros figurae intra parabolicum conoidale inscriptae, hoc est ad totam figuram inscriptam.

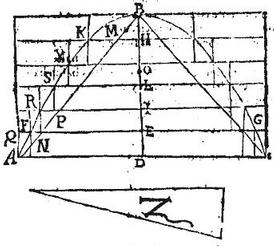
Verum per primam praemissi libelli sexcuplum basis AD plus est quam duplum aggregati reliquarum quinque basium EN, IP, HM, et cetera ergo cylindrus ABC maior est, quam duplus ad figuram inscriptam conoidi: figura autem inscripta maior fuit cono Z: igitur, et cylindrus ABC maior quam duplus ad conum Z; quod est contra hypothesim. Non est ergo maior portio conoidis ABC cono Z. Sit deinde minor: et tunc item per 8. huius, et corollarium praemissae circumscribatur portioni ABC figura quaedam ex cylindris composita, ita ut portio excedatur a figura minus, quam exceditur a cono Z: et perinde circumscripta figura sit minor cono Z; sitque maximus cylindrorum componentium dictam figuram AEC, cuius basis diameter AC, axisque ED, minimus autem cylindrus KBH, cuius basis diameter KH, axisque BH: et rursum syllogismo utere ad confutandum congruo, fere ut prius; nam sex cylindri aequales, in quos secatur cylindrus ABC ad totidem cylindros figurae circumscriptae conoidi sunt sicut sex quadrata AD ad quadrata sex ordinatarum, quae sunt semidiametri sex cylindrorum figuram componentium: sex autem quadrata AD ad quadrata sex ordinatarum sunt per 20. primi conicorum sicut sexcuplum axis BD, seu katheti ad aggregatum sex kathetorum. Et propter similitudinem triangulorum, sicut sexcuplum basis AD ad aggregatum sex basium. Hic autem adducta secunda praemissi libelli, vel 24. quinti Euclidis igitur sicut sexcuplum basis AD ad aggregatum sex basium, sic sex cylindri aequales, hoc est totus cylindrus ABC ad figuram circumscriptam. Verum per primam praemissi libelli, sexcuplum basis AD minus est, quam duplum aggregati omnium sex basium. Ergo cylindrus ABC minor est quam duplus figurae circumscriptae; figura autem circumscripta minor fuit cono Z. Igitur eo magis cylindrus ABC minor erit, quam duplus ad conum Z; quod est contra hypothesim. Non est ergo minor portio conoidis ABC cono Z; sed nec [S:255] maior fuit. Aequalis ergo erit portio solidi ABC cono Z. Et perinde sexquialtera coni ABC. Quod erat demonstrandum.