F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de conoidibus et sphaeroidibus figuris Liber primus 8
<- App. -> <- = ->

PROPOSITIO VIII.

Ellipsis ad circulum est sicut rectangulum sub ellipsis diametris contentum ad quadratum, quod ex diametro circuli.

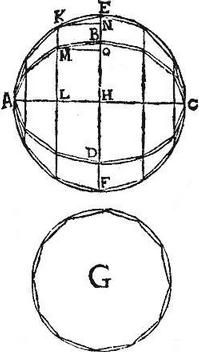
figura 8

Ellipsis est ABCD, cuius maior diameter AC, minor autem BD, circulus vero quilibet EF cuius diameter EF. Dico quod area ellipsis BD ad circulum EF est sicut rectangulum AC, BD ad quadratum EF. Describatur enim circulus super maiorem diametrum AC; eritque per praecedentem, ellipsis BD ad circulum AC, sicut linea BD ad lineam AC, sed circulus AC; ad circulum EF, sicut quadratum AC ad quadratum EF: igitur ratio ellipsis BD ad circulum EF componetur ex ratione ipsius BD ad AC, et ex dupla ratione AC ad EF; quare componetur ex ratione BD ad EF, et ex ratione AC ad EF: sed ratio rectanguli AC, BD ad quadratum EF componitur ex iisdem. Ergo ratio ellipsis BD ad circulum EF est sicut ratio rectanguli AC, BD ad quadratum EF quod erat demonstrandum. [S:233]

COROLLARIUM.

Unde si circuli diameter sit inter ellipsis diametros media proportionalis; circulus aequalis est ellipsi.

Inizio della pagina
 ->